题目内容
15.实数m分别取什么数值时,复数z=(m+2)+(3-2m)i(1)与复数12+17i互为共轭;
(2)复数的模取得最小值,求出此时的最小值.
分析 (1)根据共轭复数的定义得到关于 m的方程组,解出即可;(2)根据二次函数的性质求出|z|的最小值即可.
解答 解:(1)根据共轭复数的定义得:
$\left\{\begin{array}{l}{m+2=12}\\{3-2m=-17}\end{array}\right.$,解得:m=10;
(2)|z|=$\sqrt{{(m+2)}^{2}{+(3-2m)}^{2}}$=$\sqrt{{5(m-\frac{4}{5})}^{2}+\frac{49}{5}}$,
当m=$\frac{4}{5}$时,复数的模取最小值$\frac{7\sqrt{5}}{5}$.
点评 本题考查了复数求模问题,考查共轭复数的定义,是一道基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
3.偶函数f(x)在(0,+∞)上递增,a=f(log2$\frac{1}{3}$)b=f($\frac{3}{2}$)c=f(log32),则下列关系式中正确的是( )
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
10.函数f(x)=ax+cosx在R上是单调函数,则实数a的取值范围是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
20.如图,某组合体的三视图是由边长为2的正方形和直径为2的圆组成,则它的体积为( )


| A. | 4+4π | B. | 8+4π | C. | $4+\frac{4}{3}π$ | D. | $8+\frac{4}{3}π$ |
7.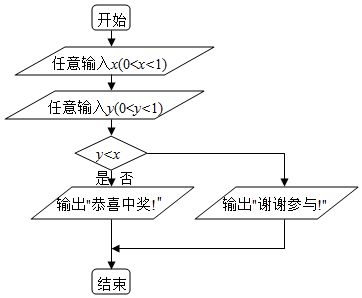 在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
 在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
3.若sinα+cosα=tan390°,则sin2α等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |