题目内容
(12分)已知函数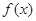 的定义域为
的定义域为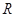 ,对于任意的
,对于任意的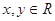 ,都有
,都有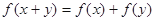 ,且当
,且当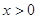 时,
时,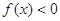 .
.
(1)求证: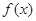 为奇函数; (2)求证:
为奇函数; (2)求证: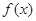 是
是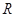 上的减函数;
上的减函数;
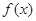 的定义域为
的定义域为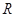 ,对于任意的
,对于任意的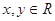 ,都有
,都有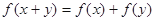 ,且当
,且当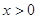 时,
时,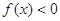 .
.(1)求证:
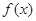 为奇函数; (2)求证:
为奇函数; (2)求证: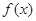 是
是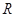 上的减函数;
上的减函数; (1)证明函数的 奇偶性,第一看定义域,第二看解析式,如果两点都满足了,则可以说明结论。
(2)而对于函数单调性的证明主要是结合定义法,作差 ,变形定号,下结论,得到结果,注意最后要化到最简。
(2)而对于函数单调性的证明主要是结合定义法,作差 ,变形定号,下结论,得到结果,注意最后要化到最简。
试题分析:(1)证明:
 的定义域为
的定义域为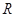 ,令
,令 ,则
,则 ,
,  令
令 ,则
,则 ,即
,即 .
. ,故
,故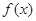 为奇函数. 6分
为奇函数. 6分(2)证明:任取
 且
且 ,
,则

又
 ,
, ,
, ,
,即
 .
.故
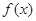 是
是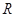 上的减函数. 12分
上的减函数. 12分点评:解决该试题的关键是对于函数奇偶性和单调性的运用,属于基础题,利用定义法来证明是常用的方法之一。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).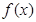 和
和 的图象关于原点对称,且
的图象关于原点对称,且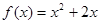 .
. 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数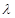 的取值范围
的取值范围 是(-
是(- 上的减函数,
上的减函数, 的取值范围是( )
的取值范围是( )



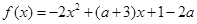 ,
,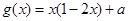 ,其中
,其中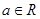 .
.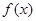 是偶函数,求函数
是偶函数,求函数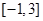 上的最小值;
上的最小值;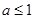 时,
时,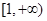 上为减函数;
上为减函数;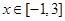 ,函数
,函数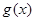 图象上方,求实数
图象上方,求实数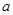 的取值范围.
的取值范围. 的连续函数
的连续函数 ,对任意
,对任意 都有
都有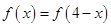 ,且其导函数
,且其导函数 满足
满足 ,则当
,则当 时,有( )
时,有( )

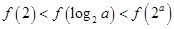

 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当 时,总有
时,总有 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数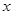 都有
都有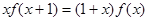 ,则
,则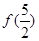 的值是( )
的值是( )



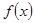 是奇函数,当
是奇函数,当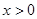 时,
时,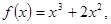 则
则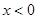 时,
时,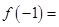 ( )
( )