题目内容
(本小题满分14分)
已知函数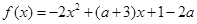 ,
,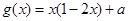 ,其中
,其中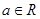 .
.
(1)若函数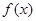 是偶函数,求函数
是偶函数,求函数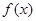 在区间
在区间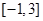 上的最小值;
上的最小值;
(2)用函数的单调性的定义证明:当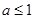 时,
时,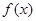 在区间
在区间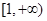 上为减函数;
上为减函数;
(3)当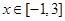 ,函数
,函数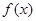 的图象恒在函数
的图象恒在函数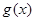 图象上方,求实数
图象上方,求实数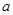 的取值范围.
的取值范围.
已知函数
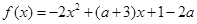 ,
,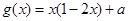 ,其中
,其中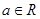 .
.(1)若函数
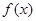 是偶函数,求函数
是偶函数,求函数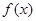 在区间
在区间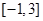 上的最小值;
上的最小值;(2)用函数的单调性的定义证明:当
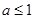 时,
时,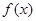 在区间
在区间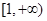 上为减函数;
上为减函数;(3)当
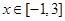 ,函数
,函数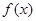 的图象恒在函数
的图象恒在函数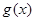 图象上方,求实数
图象上方,求实数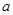 的取值范围.
的取值范围.(1)函数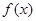 在区间
在区间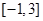 上的最小值为
上的最小值为
(2)设任意 ,且
,且 ,则利用作差法,结合变形,定号,下结论得到证明,注意变形化到最简即可。
,则利用作差法,结合变形,定号,下结论得到证明,注意变形化到最简即可。
(3)
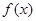 在区间
在区间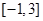 上的最小值为
上的最小值为
(2)设任意
 ,且
,且 ,则利用作差法,结合变形,定号,下结论得到证明,注意变形化到最简即可。
,则利用作差法,结合变形,定号,下结论得到证明,注意变形化到最简即可。(3)

试题分析:解:(1)
 函数
函数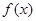 是偶函数,
是偶函数, ,
,


即函数
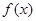 的图象是顶点为
的图象是顶点为 ,对称轴为
,对称轴为 且开口向下的抛物线,
且开口向下的抛物线, 在区间
在区间 上递增,在区间
上递增,在区间 上递减
上递减又

 函数
函数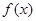 在区间
在区间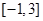 上的最小值为
上的最小值为 .
. (2)设任意
 ,且
,且 ,则
,则



又


 当
当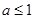 时,函数
时,函数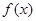 在区间
在区间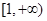 上为减函数.
上为减函数.(3)对于
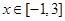 ,函数
,函数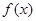 的图象恒在函数
的图象恒在函数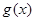 图象上方,等价不等式
图象上方,等价不等式 >
> 在
在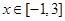 上恒成立,
上恒成立,即
 在
在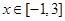 上恒成立,
上恒成立,  ,解得
,解得
 所求实数
所求实数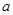 的取值范围为
的取值范围为
点评:解决的关键是根据二次函数的性质来求解证明,属于基础题。。

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 的图象为折线
的图象为折线 ,设
,设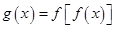 ,则函数
,则函数 的图象为( )
的图象为( )




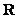 上的函数
上的函数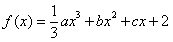 同时满足以下条件:
同时满足以下条件: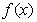 在
在 上是减函数,在
上是减函数,在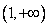 上是增函数;②
上是增函数;②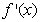 是偶函数;
是偶函数;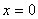 处的切线与直线
处的切线与直线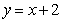 垂直.
垂直. 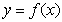 的解析式;
的解析式;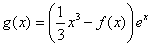 ,求函数
,求函数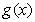 在
在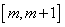 上的最小值.
上的最小值.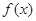 的定义域为
的定义域为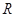 ,对于任意的
,对于任意的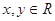 ,都有
,都有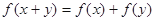 ,且当
,且当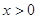 时,
时,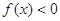 .
.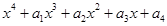
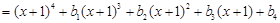 ,定义映射
,定义映射 ,则
,则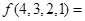 ( )
( )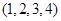
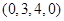
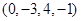
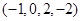
 ,若
,若 ,则
,则 =( )
=( )



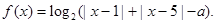
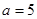 时,求函数
时,求函数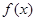 的定义域;
的定义域;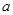 的取值范围。
的取值范围。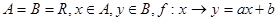 是从
是从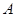 到
到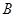 的映射,若1和8的原象分别是3和10,则5在
的映射,若1和8的原象分别是3和10,则5在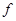 下的象是( )
下的象是( )