题目内容
17.已知x,y满足约束条件$\left\{\begin{array}{l}y≥2|x|\\ x+y-1≤0\end{array}\right.$,若z=y-ax(a>0)的最大值为3,则实数a的值为1.分析 作出x,y满足约束条件$\left\{\begin{array}{l}y≥2|x|\\ x+y-1≤0\end{array}\right.$的图象,由图象判断出最优解,令目标函数值为3,列出a的方程,求解即可.
解答 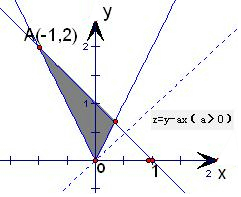 解:由题意x,y满足约束条件$\left\{\begin{array}{l}y≥2|x|\\ x+y-1≤0\end{array}\right.$,的图象如图:
解:由题意x,y满足约束条件$\left\{\begin{array}{l}y≥2|x|\\ x+y-1≤0\end{array}\right.$,的图象如图:
目标函数z=y-ax(a>0)的最大值为3,
从图象上知,
若函数z=y-ax(a>0)的最大值为3,最优解是A(-1,2),
故有2-(-1)×a=3,
则a=1,
故答案为:1.
点评 本题考查简单线性规划的应用及不等式的应用,解决本题,关键是根据线性规划的知识判断出取最值时的位置,即最优解,由此得到参数的方程,再构造出积为定值的形式求出真数的最小值.

练习册系列答案
相关题目
7.设G为等边△ABC的重心,过G作直线l分别交AB,AC(不与端点重合)于P,Q,若$\overrightarrow{AP}=λ\overrightarrow{AB}$,$\overrightarrow{AQ}=μ\overrightarrow{AC}$,若△PAG与△QAG的面积之比为$\frac{2}{3}$,则μ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
8.函数f(x)=|x-2|-kx+1有两个零点,则实数k的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,2) | C. | (2,+∞) | D. | ($\frac{1}{2}$,1) |
5.某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间相互独立,且都是整数(单位:分钟).现统计该茶楼服务员以往为100位顾客准备泡茶工具所需的时间t,结果如表所示.
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末服务员已准备好了泡茶工具的顾客数,求X的分布列及均值.
| 类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
| 顾客数(人) | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末服务员已准备好了泡茶工具的顾客数,求X的分布列及均值.
12.过点A(2,3)和点B(2,-3)的直线方程是( )
| A. | x+2=0 | B. | x-2=0 | C. | y+2=0 | D. | y-2=0 |
7.i是虚数单位,$\frac{2+i}{1+2i}$等于( )
| A. | $\frac{3}{5}$i | B. | -$\frac{3}{5}$i | C. | $\frac{4}{5}$+$\frac{3}{5}$i | D. | $\frac{4}{5}$-$\frac{3}{5}$i |