Question

【题目】各项为正的数列{an}满足 ，
（1）当λ=an+1时，求证：数列{an}是等比数列，并求其公比；
（2）当λ=2时，令 ，记数列{bn}的前n项和为Sn ， 数列{bn}的前n项之积为Tn ， 求证：对任意正整数n，2n+1Tn+Sn为定值．

Answer 1

【答案】
（1）证明：当λ=an+1时，an+1= +an，an＞0，

∴ = +1，

令 =q＞0，则q= +1，化为q2﹣q﹣1=0，解得q= ．

∴数列{an}是等比数列，其公比q= ．

（2）当λ=2时，an+1= +an，∴2an+1=an（an+2），

∴ = ．

∴Tn=b1b2b3…bn= … = = ．

又bn= = = = ﹣ ，

∴Sn=b1+b2+b3+…+bn= ﹣ + +…+ ﹣ = ﹣ ，

∴2n+1Tn+Sn= + ﹣ = =2．

∴对任意正整数n，2n+1Tn+Sn为定值2．

【解析】（1）先递推式两边同时除以an，可得含有的方程，再令=q，可得含有q的方程，解方程可得q；（2）先化简整理可得bn=，再分别计算Tn和Sn，进而可证对任意正整数n，2n+1Tn+Sn为定值．
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系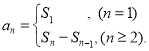；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．