题目内容
在△ABC，tanA=
，tanC=
，则∠B= ．
| 1 |
| 2 |
| 1 |
| 3 |
考点：两角和与差的正切函数
专题：计算题,三角函数的求值
分析：由tanB=tan（π-A-C）=-tan（A+C），再由两角和的正切公式，计算即可得到tanB，再由三角形的内角，即可求得B．
解答：
解：tanB=tan（π-A-C）=-tan（A+C）
=-
=-
=-1，
由于0＜B＜π，
则B=
．
故答案为：
．
=-
| tanA+tanC |
| 1-tanA•tanC |
| ||||
1-
|
=-1，
由于0＜B＜π，
则B=
| 3π |
| 4 |
故答案为：
| 3π |
| 4 |
点评：本题考查诱导公式和两角和的正切公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知椭圆
+
=1（a＞b＞0）的左顶点为A，左焦点为F，上顶点为B，且∠BAO+∠BFO=90°（O为坐标原点），则椭圆的离心率e=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
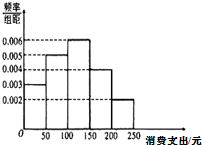已知100名学生某月饮料消费支出情况的频率分布直方图如图所示．则这100名学生中，该月饮料消费支出超过150元的人数是