题目内容
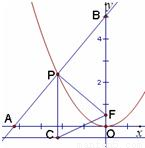
已知椭圆4x2+3y2=3,抛物线的开口向上,且其顶点在椭圆C的中心,焦点为椭圆的一个焦点F.点P为抛物线上的一点,PC垂直于直线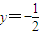 ,垂足为C,已知直线AB垂直PF分别交x、y轴于A、B.
,垂足为C,已知直线AB垂直PF分别交x、y轴于A、B.(Ⅰ)求使△PCF为等边三角形的点P坐标.
(Ⅱ)是否存在点P,使P平分线段AB,若存在求出点P,若不存在说明理由.
【答案】分析:由题意知 ,
, .抛物线方程为x2=2y,设
.抛物线方程为x2=2y,设 .
.
(Ⅰ)由题设知|PF|=|PC|,∠CFO=∠PFC=60°.故 ,所以
,所以 或
或 .
.
(Ⅱ) ,由PF⊥AB知,
,由PF⊥AB知, ,则
,则 .由此可知存在点P,使P平分线段AB.
.由此可知存在点P,使P平分线段AB.
解答:解:由4x2+3y2=3得, ,
,
所以 ,即
,即 .
.
则 ,即p=1,故抛物线方程为x2=2y,即
,即p=1,故抛物线方程为x2=2y,即 .可设
.可设 .(3分)
.(3分)
(Ⅰ)由 知,
知, 是抛物线x2=2y的准线,故|PF|=|PC|,由△PCF为等边三角形知,∠CFO=∠PFC=60°.
是抛物线x2=2y的准线,故|PF|=|PC|,由△PCF为等边三角形知,∠CFO=∠PFC=60°.
故 ,即
,即 ,即
,即 ,解得
,解得 或
或 .即
.即 或
或 .
.
故 或
或 .(6分)
.(6分)
(Ⅱ) ,由PF⊥AB知,
,由PF⊥AB知, ,则
,则 .
.
令y=0得, ,即
,即 ,
, ,
,
令x=0得, ,即
,即 ,
, .(10分)
.(10分)
若P平分线段AB,则有 且
且 ,
,
解得x2=5,即 .
.
故存在点 ,使P平分线段AB.(13分)
,使P平分线段AB.(13分)
点评:圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.除了2004年出现了两道大题(其中有一题以圆锥曲线的应用题形式出现)外,基本上是每年一道大题.除了2006年以函数的面貌,基本上还是以常态的形式出现,即以直线与圆锥曲线的位置关系的形式出现.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面向量以及导数的知识的综合命题.
 ,
, .抛物线方程为x2=2y,设
.抛物线方程为x2=2y,设 .
.(Ⅰ)由题设知|PF|=|PC|,∠CFO=∠PFC=60°.故
 ,所以
,所以 或
或 .
.(Ⅱ)
 ,由PF⊥AB知,
,由PF⊥AB知, ,则
,则 .由此可知存在点P,使P平分线段AB.
.由此可知存在点P,使P平分线段AB.解答:解:由4x2+3y2=3得,
 ,
,所以
 ,即
,即 .
.则
 ,即p=1,故抛物线方程为x2=2y,即
,即p=1,故抛物线方程为x2=2y,即 .可设
.可设 .(3分)
.(3分)(Ⅰ)由
 知,
知, 是抛物线x2=2y的准线,故|PF|=|PC|,由△PCF为等边三角形知,∠CFO=∠PFC=60°.
是抛物线x2=2y的准线,故|PF|=|PC|,由△PCF为等边三角形知,∠CFO=∠PFC=60°.故
 ,即
,即 ,即
,即 ,解得
,解得 或
或 .即
.即 或
或 .
.故
 或
或 .(6分)
.(6分)(Ⅱ)
 ,由PF⊥AB知,
,由PF⊥AB知, ,则
,则 .
.令y=0得,
 ,即
,即 ,
, ,
,令x=0得,
 ,即
,即 ,
, .(10分)
.(10分)若P平分线段AB,则有
 且
且 ,
,解得x2=5,即
 .
.故存在点
 ,使P平分线段AB.(13分)
,使P平分线段AB.(13分)点评:圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.除了2004年出现了两道大题(其中有一题以圆锥曲线的应用题形式出现)外,基本上是每年一道大题.除了2006年以函数的面貌,基本上还是以常态的形式出现,即以直线与圆锥曲线的位置关系的形式出现.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面向量以及导数的知识的综合命题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
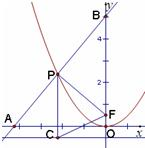 已知椭圆4x2+3y2=3,抛物线的开口向上,且其顶点在椭圆C的中心,焦点为椭圆的一个焦点F.点P为抛物线上的一点,PC垂直于直线
已知椭圆4x2+3y2=3,抛物线的开口向上,且其顶点在椭圆C的中心,焦点为椭圆的一个焦点F.点P为抛物线上的一点,PC垂直于直线