题目内容
6．数列{an}满足an+1-an+an-1=0（n≥2），且a1=1，a2=-1，则a2011=（ ）| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
分析 通过递推公式求出数列的前九项，从而确定数列周期为6，再由数列周期从而求解a2011=a1，求出结果．
解答 解：∵a1=1，a2=-1，且an+1-an+an-1=0（n≥2），
∴a3=0．a4=1，a5=-1，a6=0，a7=1，a8=-1，a9=0…
∴数列{an}是周期为3的周期函数
∴a2011=a3×670+1=a1=1．
故选：A．
点评 本题主要考查由递推公式推导数列的通项公式，其中渗透了周期数列这一知识点，属于基础题．
练习册系列答案
相关题目
1．下列函数中，与y=x-1为同一函数的是（ ）
| A． | y=$\sqrt{{{（x-1）}^2}}$ | B． | y=$\root{3}{{{{（x-1）}^3}}}$ | C． | y=$\frac{{{x^2}-1}}{x+1}$ | D． | $y={（\sqrt{x-1}）^2}$ |
11．
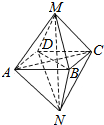如图所示的几何体，关于其结构特征，下列说法不正确的是（ ）
如图所示的几何体，关于其结构特征，下列说法不正确的是（ ）| A． | 该几何体是由两个同底的四棱锥组成的几何体 | |
| B． | 该几何体有12条棱、6个顶点 | |
| C． | 该几何体有8个面，并且各面均为三角形 | |
| D． | 该几何体有9个面，其中一个面是四边形，其余均为三角形 |