题目内容
12.已知函数f(x)=sin2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$的图象关于直线x=φ(φ|≤$\frac{π}{2}$)对称,则φ的值为( )| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | -$\frac{π}{6}$或$\frac{π}{3}$ | D. | $\frac{π}{3}$ |
分析 化简函数f(x),根据f(x)的图象关于直线x=φ(|φ|≤$\frac{π}{2}$)对称,列出方程,求出φ的值.
解答 解:∵函数f(x)=sin2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$
=$\frac{1}{2}$(1-cos2x)+$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x
=sin(2x-$\frac{π}{6}$),
且f(x)的图象关于直线x=φ(|φ|≤$\frac{π}{2}$)对称,
∴令2x-$\frac{π}{6}$=$\frac{π}{2}$+kπ,k∈Z,
解得x=$\frac{π}{3}$+$\frac{kπ}{2}$,k∈Z;
当k=0时,x=$\frac{π}{3}$,
当k=-1时,x=-$\frac{π}{6}$都满足题意,
∴φ的值为-$\frac{π}{6}$或$\frac{π}{3}$.
故选:C.
点评 本题考查了三角函数的恒等变换的应用问题,也考查了三角函数对称轴的应用问题,是基础题目.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
20.如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是( )
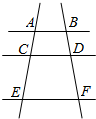

| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
7.下列关于复数的命题,正确的个数是( )
①复数a+bi与c+di的积是实数的充要条件是ad+bc=0
②命题“已知m为实数,若复数z=m+1+(m-1)i为虚数,则m≠1”的逆命题
③对于任意的z1,z2,z3∈C,有(z1•z2)•z3=z1•(z2•z3)
①复数a+bi与c+di的积是实数的充要条件是ad+bc=0
②命题“已知m为实数,若复数z=m+1+(m-1)i为虚数,则m≠1”的逆命题
③对于任意的z1,z2,z3∈C,有(z1•z2)•z3=z1•(z2•z3)
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.设函数f(x)=$\frac{2}{5}$(ex+e-x),则f(x)是( )
| A. | 奇函数 | B. | 非奇非偶函数 | ||
| C. | 偶函数 | D. | 既是奇函数又是偶函数 |