题目内容
9.已知向量$\overrightarrow a$,$\overrightarrow b$满足|$\overrightarrow a$|=2|$\overrightarrow b$|≠0,且函数在f(x)=$\frac{1}{3}{x^3}+\frac{1}{2}|\overrightarrow a|{x^2}$$+(\overrightarrow a•\overrightarrow b)x$在R上有极值,则向量$\overrightarrow a$,$\overrightarrow b$的夹角的取值范围是($\frac{π}{3}$,π).分析 由已知条件得f′(x)=x2+|$\overrightarrow{a}$|x+$\overrightarrow{a}$•$\overrightarrow{b}$=0成立,△=|$\overrightarrow{a}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$>0,由此能求出$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的取值范围.
解答 解:∵关于x的函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$|$\overrightarrow{a}$|x2+$\overrightarrow{a}$•$\overrightarrow{b}$x在R上有极值,
∴f′(x)=x2+|$\overrightarrow{a}$|x+$\overrightarrow{a}$•$\overrightarrow{b}$=0成立,方程有根,
△=|$\overrightarrow{a}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$>0,
∴|$\overrightarrow{a}$|2-4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ>0,
由|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0,得cosθ$<\frac{1}{2}$,
∴$\frac{π}{3}$<θ<π
故答案为:($\frac{π}{3}$,π).
点评 本题考查向量的夹角的取值范围的求法,是中档题,解题时要认真审题,注意根的判别式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.直线l过点P(-1,2),且倾斜角为45°,则直线l的方程为( )
| A. | x-y+1=0 | B. | x-y-1=0 | C. | x-y-3=0 | D. | x-y+3=0 |
4.有6个座位连成一片排,现有3人入座,则恰有两个空位相邻的不同坐法的种数是( )
| A. | 36 | B. | 48 | C. | 72 | D. | 120 |
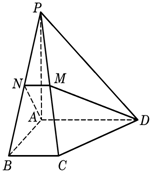 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点. 如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.
如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.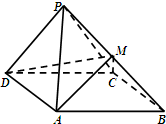 如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点. 如图四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且NB=MD=2,E为BC的中点.
如图四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且NB=MD=2,E为BC的中点.