题目内容
已知函数f(x)=x2-lnx-ax,a∈R.
(Ⅰ)若存在x∈(0,+∞),使得f(x)<0,求a的取值范围;
(Ⅱ)若f(x)=x有两个不同的实数解u,v(0<u<v),证明:f′(
)>1.
(Ⅰ)若存在x∈(0,+∞),使得f(x)<0,求a的取值范围;
(Ⅱ)若f(x)=x有两个不同的实数解u,v(0<u<v),证明:f′(
| u+v |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)当x∈(0,+∞)时,f(x)<0等价于x-
<a.由此利用导数的性质能求出a的取值范围.
(Ⅱ)由已知条件推导出a=u+v-
-1.f′(
)=
-
+1,设h(u)=lnu-lnv-
,由此利用函数的单调性能证明f′(
)>1.
| lnx |
| x |
(Ⅱ)由已知条件推导出a=u+v-
| lnu-lnv |
| u-v |
| u+v |
| 2 |
| lnu-lnv |
| u-v |
| 2 |
| u+v |
| 2(u-v) |
| u+v |
| u+v |
| 2 |
解答:
(Ⅰ)解:当x∈(0,+∞)时,f(x)<0等价于x-
<a.
令g(x)=x-
,则g′(x)=
.
当x∈(0,1)时,g′(x)<0;
当x∈(1,+∞)时,g′(x)>0.
g(x)有最小值g(1)=1.…(4分)
∴a的取值范围是(1,+∞).…(5分)
(Ⅱ)证明:∵f(x)=x,即x2-lnx=(a+1)x有两个不同的实数解u,v.
∴u2-lnu=(a+1)u,v2-lnv=(a+1)v.
∴(u+v)(u-v)-(lnu-lnv)=(a+1)(u-v).…(7分)
由u-v<0,解得a=u+v-
-1.
又f′(x)=2x-
-a,
∴f′(
)=(u+v)-
-(u+v)+
+1
=
-
+1.…(9分)
设h(u)=lnu-lnv-
,
则当u∈(0,v)时,h′(u)=
>0,
h(u)在(0,v)单调递增,h(u)<h(v)=0,
从而
-
>0,
∴f′(
)>1.(12分)
| lnx |
| x |
令g(x)=x-
| lnx |
| x |
| x2-1+lnx |
| x2 |
当x∈(0,1)时,g′(x)<0;
当x∈(1,+∞)时,g′(x)>0.
g(x)有最小值g(1)=1.…(4分)
∴a的取值范围是(1,+∞).…(5分)
(Ⅱ)证明:∵f(x)=x,即x2-lnx=(a+1)x有两个不同的实数解u,v.
∴u2-lnu=(a+1)u,v2-lnv=(a+1)v.
∴(u+v)(u-v)-(lnu-lnv)=(a+1)(u-v).…(7分)
由u-v<0,解得a=u+v-
| lnu-lnv |
| u-v |
又f′(x)=2x-
| 1 |
| x |
∴f′(
| u+v |
| 2 |
| 2 |
| u+v |
| lnu-lnv |
| u-v |
=
| lnu-lnv |
| u-v |
| 2 |
| u+v |
设h(u)=lnu-lnv-
| 2(u-v) |
| u+v |
则当u∈(0,v)时,h′(u)=
| (u-v)2 |
| u(u+v)2 |
h(u)在(0,v)单调递增,h(u)<h(v)=0,
从而
| lnu-lnv |
| u-v |
| 2 |
| u+v |
∴f′(
| u+v |
| 2 |
点评:本题考查实数的取值范围的求法,考查不等式的证明,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
相关题目

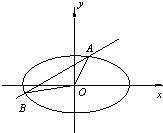 直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点).
直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点).