题目内容
8.已知$\overrightarrow a=(cosα,sinα),\overrightarrow b=(cos(-α),sin(-α))$,那么$\overrightarrow a•\overrightarrow b=0$是α=kπ+$\frac{π}{4}$(k∈Z)的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由$\overrightarrow a•\overrightarrow b=0$,可得cos2α=0,解出即可判断出结论.
解答 解:∵$\overrightarrow a•\overrightarrow b=0$=cosα•cos(-α)+sinα•sin(-α)=cos2α-sin2α=cos2α.
∴2α=$2kπ±\frac{π}{2}$,解得α=kπ±$\frac{π}{4}$(k∈Z).
∴$\overrightarrow a•\overrightarrow b=0$是α=kπ+$\frac{π}{4}$(k∈Z)的必要不充分条件.
故选:B.
点评 本题考查了向量数量积运算性质、三角函数求值、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
6.将3枚均匀的硬币各抛掷一次,恰有1枚正面朝上的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
7.根据如下样本数据
得到的回归方程为$\widehaty=\hat bx+\hat a$,则( )
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4.1 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | $\hat a>0,\hat b>0$ | B. | $\hat a>0,\hat b<0$ | C. | $\hat a<0,\hat b>0$ | D. | $\hat a<0,\hat b<0$ |
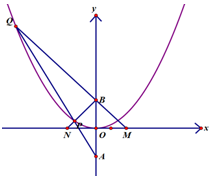 已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.
已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.