题目内容
18.用线性回归模型求得甲、乙、丙3组不同的数据对应的R2的值分别为0.81,0.98,0.63,其中乙(填甲、乙、丙中的一个)组数据的线性回归的效果最好.分析 根据两个变量y与x的回归模型中,它们的相关指数R2越接近于1,这个模型的拟合效果越好,由此得出答案.
解答 解:两个变量y与x的回归模型中,它们的相关指数R2越接近于1,
这个模型的拟合效果就越好,
在甲、乙、丙中,所给的数值中0.98是相关指数最大的值,
即乙的拟合效果最好.
故答案为:乙.
点评 本题考查了相关指数的应用问题,解题的关键是理解相关指数越大其拟合效果越好.

练习册系列答案
相关题目
9.已知$sin(\frac{π}{3}-α)=\frac{1}{4}$,则$cos(\frac{π}{3}+2α)$=( )
| A. | $\frac{5}{8}$ | B. | $-\frac{7}{8}$ | C. | $-\frac{5}{8}$ | D. | $\frac{7}{8}$ |
10.已知椭圆C1与双曲线C2有相同的左右焦点F1、F2,P为椭圆C1与双曲线C2在第一象限内的一个公共点,设椭圆C1与双曲线C2的离心率为e1,e2,且$\frac{{e}_{1}}{{e}_{2}}$=$\frac{1}{3}$,若∠F1PF2=$\frac{π}{3}$,则双曲线C2的渐近线方程为( )
| A. | x±y=0 | B. | x±$\frac{\sqrt{3}}{3}$y=0 | C. | x±$\frac{\sqrt{2}}{2}$y=0 | D. | x±2y=0 |
8.已知$\overrightarrow a=(cosα,sinα),\overrightarrow b=(cos(-α),sin(-α))$,那么$\overrightarrow a•\overrightarrow b=0$是α=kπ+$\frac{π}{4}$(k∈Z)的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
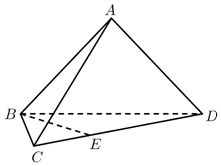 如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.
如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.