题目内容
若f（2x）=log2
，则f（1）=（ ）
| 4x+10 |
| 3 |
| A、2 | ||
B、
| ||
| C、1 | ||
D、log2
|
考点：函数的值
专题：函数的性质及应用
分析：由函数的性质得f（1）=f（2×
）=log2
=log24=2．
| 1 |
| 2 |
4×
| ||
| 3 |
解答：
解：∵f（2x）=log2
，
∴f（1）=f（2×
）=log2
=log24=2．
故选：A．
| 4x+10 |
| 3 |
∴f（1）=f（2×
| 1 |
| 2 |
4×
| ||
| 3 |
故选：A．
点评：本题考查函数值的求法，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
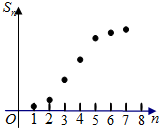某工厂前n年的总产量Sn与n之间的关系如图所示．从目前记录的结果看，前m年的年平均产量最高．m值为（ ）| A、2 | B、4 | C、5 | D、8 |
设等比数列{an}的前n项和为Sn，若S10：S5=1：2，则
=（ ）
| S5+S10+S15 |
| S10-S5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知奇函数f（x）当x＞0时，f（x）=x（1-x），则当x＜0时，f（x）的表达式是（ ）
| A、-x（1-x） |
| B、x（1+x） |
| C、-x（1+x） |
| D、x（1-x） |
已知直线l：3x-y+6=0，则直线l在x轴上的截距是（ ）
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
| D、-2 |