题目内容
对于任意实数x,符号[x]表示x的整数部分,即[x]是不超过x的最大整数,例如[2]=2;[2.1]=2;[-2.2]=-3,这个函数[x]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用.那么[log21]+[log22]+[log23]+…+[log216]的值为( )
| A、21 | B、34 | C、35 | D、38 |
考点:对数的运算性质,函数的值
专题:函数的性质及应用
分析:根据“取整函数”,分别计算出[log21]=0,[log22]=[log23]=1,[log24]=[log25]=…=[log27]=2,然后根据整数的个数即可计算出函数的值.
解答:
解:由于[log21]=[0]=0,有1个0
[log22]=[log23]=1.有2个1
[log24]=[log25]=[log26]=[log27]=2.有4个2
[log28]=[log29]=[log210]=…=[log215]=3,有8个3,
[log216]=4,有1个4.
∴[log21]+[log22]+[log23]+…+[log216]=0+1×2+2×4+8×3+4×1=38.
故选:D.
[log22]=[log23]=1.有2个1
[log24]=[log25]=[log26]=[log27]=2.有4个2
[log28]=[log29]=[log210]=…=[log215]=3,有8个3,
[log216]=4,有1个4.
∴[log21]+[log22]+[log23]+…+[log216]=0+1×2+2×4+8×3+4×1=38.
故选:D.
点评:本题考查新定义的应用,主要考查了对数的函数值的求解,解题的关键是把所给的对数值正确取整,确定整数的个数.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的三只球中的最小号码,则P(ξ=2)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式(x2-4)(x-6)2≤0的解集为( )
| A、{x|-2≤x≤2} |
| B、{x|x≥2或x≤-2} |
| C、{x|-2≤x≤2或x=6} |
| D、{x|x≥2} |
设a=0.6
,b=0.7
,c=lg
,则a,b,c之间的关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、c<a<b |
| B、b<a<c |
| C、c<b<a |
| D、a<b<c |
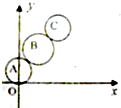 我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”.在如图所示的“串圆”中,⊙A和⊙C的方程分别为x2+(y-1)2=2和(x-6)2+(y-7)2=2,则⊙B的方程为
我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”.在如图所示的“串圆”中,⊙A和⊙C的方程分别为x2+(y-1)2=2和(x-6)2+(y-7)2=2,则⊙B的方程为