题目内容
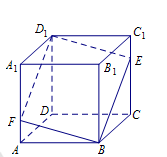
如图所示,在正方体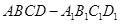 中,点
中,点 是棱
是棱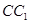 上的一个动点,平面
上的一个动点,平面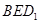 交棱
交棱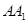 于点
于点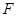 .则下列命题中假命题是( )
.则下列命题中假命题是( )
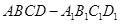 中,点
中,点 是棱
是棱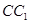 上的一个动点,平面
上的一个动点,平面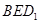 交棱
交棱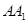 于点
于点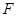 .则下列命题中假命题是( )
.则下列命题中假命题是( )
A.存在点 ,使得 ,使得 //平面 //平面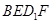 |
B.存在点 ,使得 ,使得 平面 平面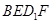 |
C.对于任意的点 ,平面 ,平面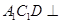 平面 平面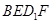 |
D.对于任意的点 ,四棱锥 ,四棱锥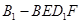 的体积均不变 的体积均不变 |
B
试题分析:当点
 为
为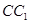 的中点时,由对称性可知
的中点时,由对称性可知 也是
也是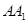 的中点,此时
的中点,此时 //
// ,因为
,因为 ,
, ,所以
,所以 //
// ,故A正确;
,故A正确;假设
 ,因为
,因为 ,所以
,所以 。所以四边形
。所以四边形 为菱形或正方形,即
为菱形或正方形,即 。因为
。因为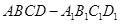 为正方体所以
为正方体所以 。所以假设不成立。故B不正确。
。所以假设不成立。故B不正确。因为
 为正方形,所以
为正方形,所以 ,因为
,因为 ,
, ,所以
,所以 ,因为
,因为 ,所以
,所以 。因为
。因为 ,所以
,所以 。同理可证
。同理可证 ,因为
,因为 ,所以
,所以 ,因为
,因为 ,所以
,所以 。故C正确。
。故C正确。设正方体边长为
 ,则
,则 。故D正确。
。故D正确。
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
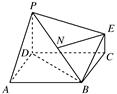
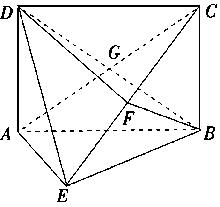
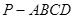 中,底面
中,底面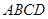 为矩形,
为矩形,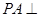 平面
平面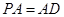 ,
,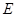 为
为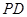 中点.
中点.
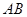 //平面
//平面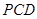 ;
;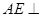 平面
平面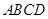 中,
中,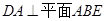 ,
,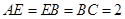 ,
,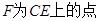 ,且
,且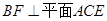 ,
,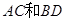 交于点
交于点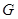 .
.
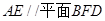 ;
;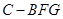 的体积.
的体积. 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
 平面
平面
 平面
平面 .
.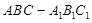 中,
中,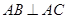 ,
,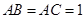 ,
,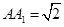 ,D为BC中点.
,D为BC中点.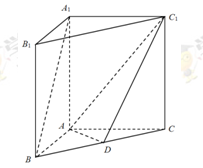
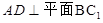 ;
; ;
;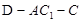 的正弦值.
的正弦值.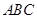 的直角边
的直角边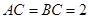 ,沿其中位线
,沿其中位线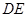 将平面
将平面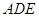 折起,使平面
折起,使平面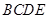 ,得到四棱锥
,得到四棱锥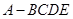 ,设
,设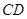 、
、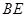 、
、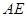 、
、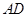 的中点分别为
的中点分别为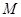 、
、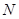 、
、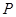 、
、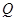 .
.


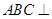 平面
平面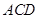 ;
;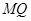 所成的角.
所成的角. 中,
中, 分别是
分别是 的中点,则四边形
的中点,则四边形 是( )
是( )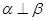 ,
,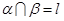 ,直线
,直线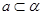 ,直线
,直线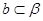 ,
,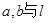 斜交,则( )
斜交,则( )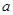 和
和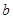 不垂直但可能平行
不垂直但可能平行