题目内容
3．底面半径为$\sqrt{3}$，高为2的圆锥的体积为2π．分析 底面半径为$\sqrt{3}$，高为2的圆锥的体积为：$V=\frac{1}{3}Sh$=$\frac{1}{3}×π{r}^{2}h$，由此能求出结果．
解答 解：底面半径为$\sqrt{3}$，高为2的圆锥的体积为：
$V=\frac{1}{3}Sh$=$\frac{1}{3}×π{r}^{2}h$=$\frac{1}{3}π×（\sqrt{3}）^{2}×2$=2π．
故答案为：2π．
点评 本题考查圆锥的体积的求法，是基础题，解题时要认真审题，注意体积公式的合理运用．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
18．
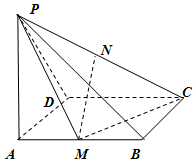如图，PA⊥矩形ABCD所在的平面，PA=AD，且M，N分别是AB，PC的中点．
（1）求证：MN∥平面PAD；
（2）求证：MN⊥平面PCD；
（3）若PA=2，AB=4，求三棱锥B-PMC的体积．
如图，PA⊥矩形ABCD所在的平面，PA=AD，且M，N分别是AB，PC的中点．（1）求证：MN∥平面PAD；
（2）求证：MN⊥平面PCD；
（3）若PA=2，AB=4，求三棱锥B-PMC的体积．
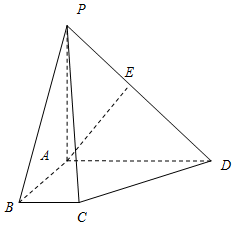在四棱锥P-ABCD中，底面ABCD是一直角梯形，PA⊥底面ABCD，∠BAD=90°，AP⊥BC，AB=BC=1，AD=AP=2，E是PD的中点．
12．命题“?x0∈∁RQ，x03∈Q”的否定是（ ）
| A． | ?x0∉∁RQ，x03∈Q | B． | ?x0∈∁RQ，x03∈Q | C． | ?x∉∁RQ，x3∈Q | D． | ?x∈∁RQ，x3∉Q |
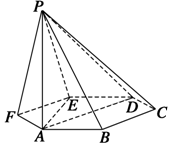如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论正确的序号是④．