题目内容
4.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左焦点向圆x2+y2=a2作一条切线,若该切线与双曲线的两条渐进线分别相交于第一、二象限,且被双曲线的两条渐进线截得的线段长为$\sqrt{3}a$,则该双曲线的离心率为2.分析 由题意,过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左焦点向圆x2+y2=a2作一条切线,斜率为$\frac{a}{b}$,与渐近线y=-$\frac{b}{a}$x垂直,利用被双曲线的两条渐进线截得的线段长为$\sqrt{3}a$,可得两条渐近线的夹角为60°,即可得出结论.
解答 解:由题意,过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左焦点
向圆x2+y2=a2作一条切线,斜率为$\frac{a}{b}$,与渐近线y=-$\frac{b}{a}$x垂直,
∵被双曲线的两条渐进线截得的线段长为$\sqrt{3}a$,
∴两条渐近线的夹角为60°,
∴$\frac{b}{a}$=$\sqrt{3}$,∴c=2a,
∴e=$\frac{c}{a}$=2.
故答案为2.
点评 本题考查直线与圆、双曲线的位置关系,考查双曲线的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.下列函数中,其定义域和值域与函数y=elnx的定义域和值域相同的是( )
| A. | y=x | B. | y=lnx | C. | y=$\frac{1}{\sqrt{x}}$ | D. | y=10x |
19.已知$tan({α+\frac{π}{4}})=\frac{3}{4}$,则${cos^2}({\frac{π}{4}-α})$=( )
| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{24}{25}$ |
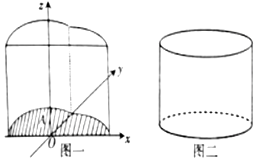 我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.
我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.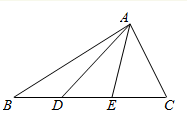 如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.
如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.