题目内容
已知函数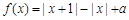 .
.
(Ⅰ)若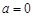 ,求不等式
,求不等式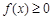 的解集;
的解集;
(Ⅱ)若方程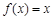 有三个不同的解,求
有三个不同的解,求 的取值范围.
的取值范围.
(Ⅰ)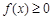 的解集为
的解集为 ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)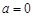 时,
时,
 ,
,
∴当 时,
时, 不合题意;
不合题意;
当 时,
时, ,解得
,解得 ;
;
当 时,
时, 符合题意. 3分
符合题意. 3分
综上,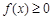 的解集为
的解集为 5分
5分
(Ⅱ)设 ,
, 的图象和
的图象和 的图象如图: 7分
的图象如图: 7分
易知 的图象向下平移1个单位以内(不包括1个单位)与
的图象向下平移1个单位以内(不包括1个单位)与 的图象始终有3个交点,
的图象始终有3个交点,
从而 . 10分
. 10分
考点:本题主要考查绝对值的概念,分段函数的概念,绝对值不等式的解法。
点评:中档题,涉及绝对值问题,一般要考虑“去绝对值符号”,常用方法是:平方法、分类讨论法。本题(II)将问题转化成研究函数图象的交点,实现了“化难为易”。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 表示
表示 导函数。
导函数。 为奇数时,设
为奇数时,设 ,数列
,数列 的前
的前 项和为
项和为 ,证明不等式
,证明不等式 对一切正整数
对一切正整数 与
与 的大小.
的大小.
 时,求函数
时,求函数 的极值;
的极值; 时,讨论函数
时,讨论函数 及任意
及任意 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 的图象;
的图象;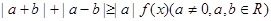 恒成立,求实数
恒成立,求实数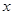 的范围.
的范围.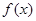 是
是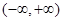 上的增函数,
上的增函数,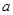 ,
,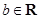 .
. ,求证:
,求证: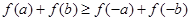 ;
;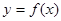 在
在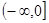 上递增,函数f(x)的一个零点为
上递增,函数f(x)的一个零点为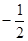 ,
,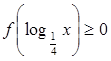 的x的取值集合.
的x的取值集合. 是定义在
是定义在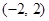 上的奇函数且是减函数,若
上的奇函数且是减函数,若 ,求实数
,求实数 的取值范围。
的取值范围。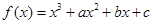 在
在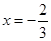 与
与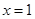 时都取得极值.
时都取得极值. 的值与函数
的值与函数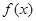 的单调区间
的单调区间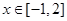 ,不等式
,不等式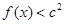 恒成立,求
恒成立,求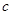 的取值范围。
的取值范围。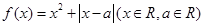 .
.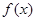 的奇偶性;
的奇偶性;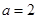 时,求
时,求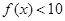 对
对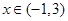 恒成立,求实数
恒成立,求实数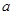 的取值范围.
的取值范围.