题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{1-x},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$,若|f(a)|≥2,则实数a的取值范围是$({-∞,\frac{1}{2}}]∪[{8,+∞})$.分析 根据解析式对a分类讨论,分别列出不等式后,由指数、对数函数的性质求出实数a的取值范围.
解答 解:由题意知,f(x)=$\left\{\begin{array}{l}{{2}^{1-x},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$,
①当a≤0时,不等式|f(a)|≥2为|21-a|≥2,
则21-a≥2,即1-a≥1,解得a≤0;
②当a>0时,不等式|f(a)|≥2为$|1-lo{g}_{2}^{a}|≥2$,
则$1-lo{g}_{2}^{a}≥2$或$1-lo{g}_{2}^{a}≤-2$,
即$lo{g}_{2}^{a}≤-1$或$lo{g}_{2}^{a}≥3$,解得0<a $≤\frac{1}{2}$或a≥8;
综上可得,实数a的取值范围是$(-∞,\frac{1}{2}]∪[8,+∞)$,
故答案为:$(-∞,\frac{1}{2}]∪[8,+∞)$.
点评 本题考查利用分段函数求不等式的解集,以及指数、对数函数的性质的应用,考查分类讨论思想,化简、变形能力.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
12.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面 的4个图形中,能表示集合M到集合N的函数关系的有( )
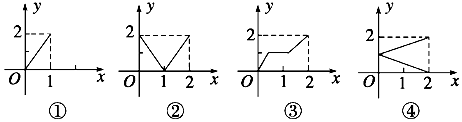
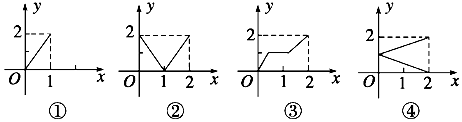
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
16.已知双曲线C$:\frac{x^2}{a^2}-\frac{y^2}{4}=1$的一条渐近线方程为2x+3y=0,F1,F2分别是双曲线C的左,右焦点,点P在双曲线C上,且|PF1|=7,则|PF2|等于( )
| A. | 1 | B. | 13 | C. | 4或10 | D. | 1或13 |
6.已知复数z的实部为-1,虚部为2,则$\frac{5i}{\overline z}$对应的点位于( )
| A. | 第四象限 | B. | 第一象限 | C. | 第三象限 | D. | 第二象限 |
13.已知集合{x|x2+ax=0}={0,1},则实数a的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
7.若函数y=|x-2|-2的定义域为集合M={x∈R|-2≤x≤2},值域为集合N,则( )
| A. | M=N | B. | M?N | C. | N?M | D. | M∩N=∅ |
8.过点(2,3)的直线l被两平行线L1:2x-5y+9=0与L2:2x-5y-7=0所截线段AB的中点恰在直线x-4y-1=0上,则直线l的方程为( )
| A. | 4x-5y+7=0 | B. | 5x-4y+11=0 | C. | 2x-3y-4=0 | D. | 4x+5y-23=0 |
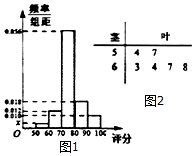 某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.
某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.