题目内容
19．已知直线l1：（3+m）x+4y=4，l2：2x+（5+m）y=8平行，实数m的值为（ ）| A． | -7 | B． | -1 | C． | $\frac{13}{3}$ | D． | -1或-7 |
分析 由（3+m）（5+m）-8=0，解得m．经过验证是否满足条件即可得出．
解答 解：由（3+m）（5+m）-8=0，化为：m2+8m+7=0，解得m=-1，-7．
经过验证满足条件．
故选：D．
点评 本题考查了两条直线平行的充要条件、方程的解法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．已知$\frac{1-tanα}{1+tanα}$=2+$\sqrt{3}$，则tan（$\frac{π}{4}$+α）等于（ ）
| A． | 2+$\sqrt{3}$ | B． | 1 | C． | 2-$\sqrt{3}$ | D． | $\sqrt{3}$ |
7．△ABC的三内角A，B，C所对边的长分别是a，b，c，若$\frac{sinB-sinA}{sinC}=\frac{{\sqrt{2}a+c}}{a+b}$，则角B的大小为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
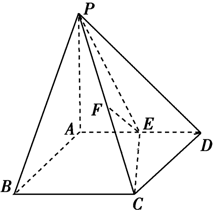如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为正方形，且PA=AD=2，E、F分别为棱AD、PC的中点．