题目内容
8.若|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{2}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{10}$.分析 根据向量的数量积的运算和模的计算即可求出.
解答 解:∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{2}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$$\overrightarrow{b}$=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=4+2+2×2×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=10,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{10}$,
故答案为:$\sqrt{10}$
点评 本题考查了向量的数量积的运算和模的计算,关键是掌握数量积公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上的函数
上的函数 满足:①当
满足:①当 时,函数
时,函数 ;②函数
;②函数 的图象关于点
的图象关于点 对称,则不等式
对称,则不等式 的解集为( )
的解集为( ) B.
B.
 D.
D.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
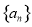 的前
的前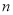 项和为
项和为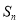 ,且满足
,且满足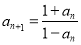 ,若
,若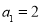 ,则
,则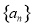 的前2017项的积为( )
的前2017项的积为( ) 是函数
是函数 图象的一条切线,则
图象的一条切线,则 ( )
( ) C.2 D.
C.2 D.