题目内容
6.已知函数y=f(x)对任意自变量x都有f(x)=f(2-x),且函数f(x)在[1,+∞)上单调.若数列{an}是公差不为0的等差数列,且f(a6)=f(a2012),则{an}的前2017项之和为( )| A. | 0 | B. | 2017 | C. | 2016 | D. | 4034 |
分析 函数y=f(x)对任意自变量x都有f(x)=f(2-x),且函数f(x)在[1,+∞)上单调.由f(a6)=f(a2012),可得a6+a2012=2,再利用等差数列的通项公式及其性质、求和公式即可得出.
解答 解:∵函数y=f(x)对任意自变量x都有f(x)=f(2-x),且函数f(x)在[1,+∞)上单调.
∵f(a6)=f(a2012),∴a6+a2012=2,
又数列{an}是公差不为0的等差数列,
∴a6+a2012=a1+a2017,
则{an}的前2017项之和=$\frac{2017({a}_{1}+{a}_{2017})}{2}$=2017×$\frac{2}{2}$=2017.
故选:B.
点评 本题考查了函数的对称性、等差数列的通项公式及其性质、求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
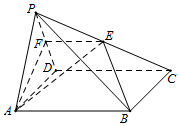 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,$BD=2\sqrt{2}$,E、F分别为AD、PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,$BD=2\sqrt{2}$,E、F分别为AD、PC中点.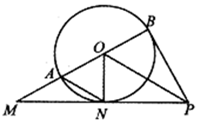 如图所示,已知AB为⊙O的直径,PB、PN都是⊙O的切线,切点分别为B、N,PN交BA的延长线于点M.
如图所示,已知AB为⊙O的直径,PB、PN都是⊙O的切线,切点分别为B、N,PN交BA的延长线于点M.