题目内容
数列{an}的前n项和为sn，sn=an2+bn+c（a，b，c∈R，n∈N+）则“c=0”是{an}为等差数列的（ ）
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：等差数列与等比数列
分析：根据充分必要条件的定义结合等差数列的性质，从而得到答案．
解答：
解：当c=0时，an=Sn-Sn-1=（an2+bn）-[a（n-1）2+b（n-1）]
=（an2+bn）-（an2-2an+a+bn-b）=2an-a+b．
∴a2-a1=（4a-a）-（2a-a）=2a，
∴c=0时，数列{an}为等差数列，
是充分条件；
若数列{an}是等差数列，则sn=na1+
=
n2+（a1-
）n=an2+bn+c，
∴c=0，是必要条件，
故选：B．
=（an2+bn）-（an2-2an+a+bn-b）=2an-a+b．
∴a2-a1=（4a-a）-（2a-a）=2a，
∴c=0时，数列{an}为等差数列，
是充分条件；
若数列{an}是等差数列，则sn=na1+
| n(n-1)d |
| 2 |
| d |
| 2 |
| d |
| 2 |
∴c=0，是必要条件，
故选：B．
点评：本题考查数列的性质和应用，解题要认真审题，仔细解答．
练习册系列答案
相关题目
下列各组函数中，两个函数相等的是（ ）
A、f（x）=
| |||||||
B、f（x）=
| |||||||
C、f（x）=（
| |||||||
D、f（x）=
|
等比数列{an}中，a2=3，a5=
，则公比q=（ ）
| 1 |
| 9 |
| A、3 | ||
B、
| ||
| C、±3 | ||
D、±
|
已知{an}是等比数列，a1=1，a3=2，则a2=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
下列函数中最小正周期为2π的函数是（ ）
A、y=sin(x-
| ||
B、y=cos(2x+
| ||
C、y=cos(3x-
| ||
D、y=tan(x-
|
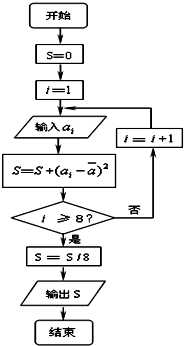对一个作直线运动的质点的运动过程观测了8次，第i次观测得到的数据为