题目内容
已知椭圆
（a＞b＞0）的离心率为
，且过点（
）．
（1）求椭圆E的方程；
（2）设直线l:y=kx+t与圆
（1＜R＜2）相切于点A，且l与椭圆E只有一个公共点B.
①求证：
；
②当R为何值时，
取得最大值？并求出最大值．
（a＞b＞0）的离心率为，且过点（）．（1）求椭圆E的方程；
（2）设直线l:y=kx+t与圆
（1＜R＜2）相切于点A，且l与椭圆E只有一个公共点B.①求证：
；②当R为何值时，
取得最大值？并求出最大值．(1)
；（2）①证明见解析；②
时，取得最大值为1．
；（2）①证明见解析；②时，取得最大值为1．试题分析：(1)椭圆的离心率为
，又椭圆过已知点，即
，再加上
，联立可求得
；（2）直线与圆及椭圆都相切，因此可以把直线方程与椭圆方程(或圆方程)联立方程组，此方程组只有一解，由此可得到题中参数的关系式，当然直线与圆相切，可利用圆心到直线的距离等于圆的半径来列式，得到的两个等式中消去参数
即可证得①式；而②要求
的最大值，可先求出，注意到
，因此
，这里设
，由①中的方程(组)可求得
，最终把用
表示，
，利用不等式知识就可求得最大值.试题解析：(1)椭圆E的方程为
4分（2）①因为直线
与圆C:
相切于A,得
,即
① 5分又因为
与椭圆E只有一个公共点B，由
得
,且此方程有唯一解.则
即
②由①②,得
8分②设
，由
得
由韦达定理,
∵
点在椭圆上,∴
∴
10分在直角三角形OAB中,
∴
12分
练习册系列答案
通城学典默写能手系列答案
相关题目
的右焦点为F，A为短轴的一个端点，且
，
的面积为1（其中
为坐标原点）.
，连结CM，交椭圆于点
，证明：
为定值；
轴上是否存在异于点C的定点Q，使得以MP为直径的圆恒过直线DP、MQ的交点，若存在，求出点Q的坐标；若不存在，说明理由.
：
的离心率为
，右焦点为(
，0)．
作两条互相垂直的射线，与椭圆交于
，
两点，求证：点
的距离为定值.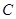
的中心在原点
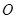，焦点在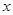
轴上，离心率为
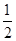，右焦点到右顶点的距离为
．
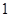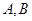两点的直线
：
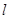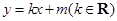，使得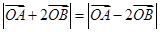
成立？若存在，求出实数
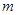的取值范围，若不存在，请说明理由.
的离心率
，连接椭圆的四个顶点得到的菱形的面积为4．
与椭圆相交于不同的两点
，已知点
的坐标为
，点
在线段
的垂直平分线上，且
，求
的值.
轴上，且长轴长为12，离心率为
，则椭圆的方程是( )
PF1F2是以PF1为底边的等腰三角形，若椭圆与双曲线的离心率分别为e1，e2，则e1·e2的取值范围是( )
，+
) 
，+
，+
有公共焦点，且离心率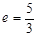
的双曲线方程是（ ）
（
），若椭圆的离心率
，则
的取值范围是.