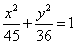题目内容
已知椭圆 的离心率
的离心率 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 ,求
,求 的值.
的值.
 的离心率
的离心率 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程;
(2)设直线
 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 ,求
,求 的值.
的值.(1)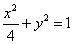 (2)
(2)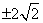 或
或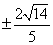
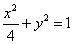 (2)
(2)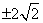 或
或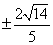
(1)由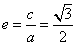 ,得
,得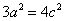 ,再由
,再由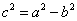 ,得
,得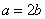
由题意可知,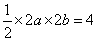 即
即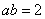 .
.
解方程组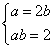 得
得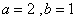 ,所以椭圆的方程为
,所以椭圆的方程为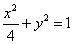 .
.
(2)解:由(1)可知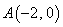 .设B点的坐标为
.设B点的坐标为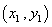 ,直线l的斜率为k,则直线l的方程为
,直线l的斜率为k,则直线l的方程为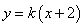 ,
,
于是A,B两点的坐标满足方程组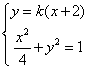
由方程组消去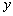 整理,得
整理,得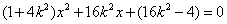
由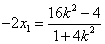 得
得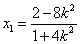
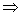
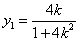
设线段AB是中点为M,则M的坐标为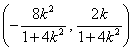 ,
,
以下分两种情况:
(1)当k=0时,点B的坐标为(2,0).
此时线段AB的垂直平分线为y轴,于是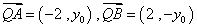
∵ ,∴
,∴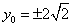
(2)当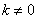 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为
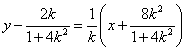
令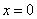 ,解得
,解得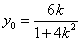
由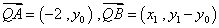
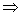
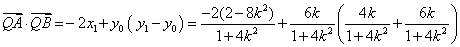
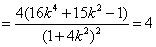
整理得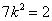 ,∴
,∴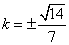
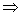
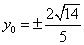
综合知: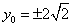 或
或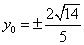
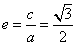 ,得
,得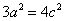 ,再由
,再由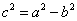 ,得
,得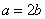
由题意可知,
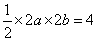 即
即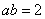 .
.解方程组
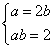 得
得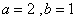 ,所以椭圆的方程为
,所以椭圆的方程为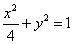 .
.(2)解:由(1)可知
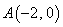 .设B点的坐标为
.设B点的坐标为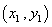 ,直线l的斜率为k,则直线l的方程为
,直线l的斜率为k,则直线l的方程为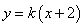 ,
,于是A,B两点的坐标满足方程组
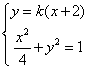
由方程组消去
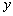 整理,得
整理,得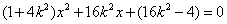
由
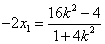 得
得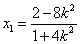
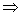
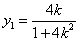
设线段AB是中点为M,则M的坐标为
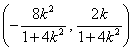 ,
,以下分两种情况:
(1)当k=0时,点B的坐标为(2,0).
此时线段AB的垂直平分线为y轴,于是
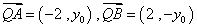
∵
 ,∴
,∴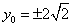
(2)当
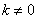 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为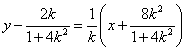
令
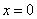 ,解得
,解得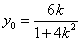
由
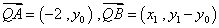
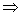
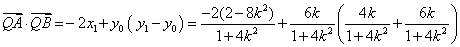
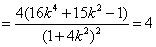
整理得
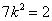 ,∴
,∴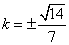
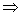
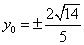
综合知:
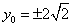 或
或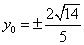

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且过点(
,且过点( ).
). (1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
(1<R<2)相切于点A,且l与椭圆E只有一个公共点B. ;
; 取得最大值?并求出最大值.
取得最大值?并求出最大值.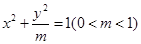 的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
 ,求m的值;
,求m的值; ,求m的取值范围.
,求m的取值范围. 中,如图,已知椭圆E:
中,如图,已知椭圆E: 的左、右顶点分别为
的左、右顶点分别为 、
、 ,上、下顶点分别为
,上、下顶点分别为 、
、 .设直线
.设直线 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆 与以线段
与以线段 为直径的圆关于直线
为直径的圆关于直线
 ,求圆
,求圆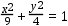 内一点R(1,0)作动弦MN,则弦MN中点P的轨迹是( )
内一点R(1,0)作动弦MN,则弦MN中点P的轨迹是( ) 内接于椭圆
内接于椭圆 ,且
,且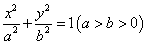 的左,右焦点分别为
的左,右焦点分别为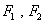 ,P为椭圆M上任一点,且
,P为椭圆M上任一点,且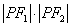 的最大值的取值范围是
的最大值的取值范围是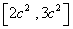 ,其中
,其中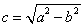 ,则椭圆M的离心率e的取值范围是________.
,则椭圆M的离心率e的取值范围是________. 的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( )
的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( )