题目内容
已知正三棱锥P-ABC中，PA=PB=PC=1，且PA，PB，PC两两垂直，则该三棱锥外接球的表面积为 ．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P-ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P-ABC外接球的表面积．
解答：
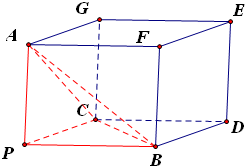解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为
，
∴球半径R=
，
因此，三棱锥P-ABC外接球的表面积是4πR2=4π×（
）2=3π
故答案为：3π．
解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为
| 3 |
∴球半径R=
| ||
| 2 |
因此，三棱锥P-ABC外接球的表面积是4πR2=4π×（
| ||
| 2 |
故答案为：3π．
点评：本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．
练习册系列答案
相关题目
直线OA，OB，OC两两垂直，直线OP与直线OA，OB，OC所成的角相等，则直线OP与面OAB的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果直线a和b没有公共点，那么a与b（ ）
| A、共面 |
| B、平行 |
| C、可能平行，也可能是异面直线 |
| D、是异面直线 |
下列有关命题的叙述错误的是（ ）
| A、对于命题p：?x0∈R，x02+x0+1＜0，则￢p为：?x∈R，x2+x+1≥0 |
| B、若p∧q为假命题，则p，q均为假命题 |
| C、命题“若x2-3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2-3x+2≠0” |
| D、x2-5x+6=0是x=2的必要不充分条件 |