题目内容
1．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+kx，x≤1}\\{2{x}^{2}，x＞1}\end{array}\right.$，若存在a，b∈R，且a≠b，使得f（a）=f（b）成立，则实数k的取值范围是k＜2，或k＞3．分析 依题意，在定义域内，f（x）不是单调函数．结合二次函数的图象和性质及分段函数的单调性，可得结论．
解答 解：依题意，在定义域内，f（x）不是单调函数．
由f（x）=2x2，x＞1为增函数，且x=1时，2x2=2得：
x≤1时，$\frac{k}{2}＜1$，或-1+k＞2，
解得：k＜2，或k＞3，
故答案为：k＜2，或k＞3
点评 本题考查的知识点是分段函数的应用，分类讨论思想，难度中档．
练习册系列答案
相关题目
12．
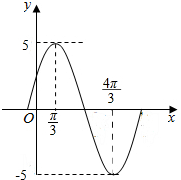函数f（x）=$\sqrt{{a}^{2}+{b}^{2}}$sin（ωx+φ），x∈R，其中a，b，ω都为正数，在一个周期内的图象如图，满足f（x）＜$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是（ ）
函数f（x）=$\sqrt{{a}^{2}+{b}^{2}}$sin（ωx+φ），x∈R，其中a，b，ω都为正数，在一个周期内的图象如图，满足f（x）＜$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是（ ）| A． | （-∞，2kπ），k∈Z | B． | （2kπ-π，2kπ），k∈Z | C． | （2kπ-2π，2kπ），k∈Z | D． | （2kπ-$\frac{4π}{3}$，2kπ），k∈Z |
6．任取k∈[-1，1]，直线L：y=kx+3与圆C：（x-2）2+（y-3）2=4相交于M、N两点，则|MN|≥2$\sqrt{3}$的概率为 （ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |