题目内容
16.若集合A={x|(x+1)(x-10)<0},B={y∈N|y<6},则A∩B等于( )| A. | ∅ | B. | (-1,6) | C. | {1,2,3,4,5} | D. | {0,1,2,3,4,5} |
分析 先化简集合A,B,再根据交集的定义即可求出.
解答 解:集合A={x|(x+1)(x-10)<0}={x|-1<x<10},B={y∈N|y<6}={0,1,2,3,4,5,6},
则A∩B={0,1,2,3,4,5},
故选:D.
点评 本题考查了不等式的解法和集合的交集的运算,属于基础题.

练习册系列答案
相关题目
6.在样本的频率分布直方图中,一共有m(m≥3)个小矩形,第3个小矩形的面积等于其余m-1各小矩形面积之和的$\frac{1}{4}$,且样本容量为100,则第3组的频数是( )
| A. | 10 | B. | 20 | C. | 25 | D. | 40 |
4.已知变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y-1≤0}\\{x-y-1≤0}\\{x-a≥0}\end{array}}\right.$,若$|{\frac{y}{x-2}}|≤\frac{1}{2}$,则实数a的取值范围是( )
| A. | (0,1] | B. | [0,1) | C. | [0,1] | D. | (0,1) |
1.设全集U=R,A={x|0.3x<1},B={x|x<x2-2},则A∩(∁UB)=( )
| A. | {x|-1<x<0} | B. | {x|0<x≤2} | C. | {x|0<x<2} | D. | {x|0<x≤1} |
8.函数f(x)=2sin(ωx+φ)(w>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)+f($\frac{17π}{12}$)的值为( )
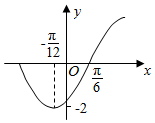
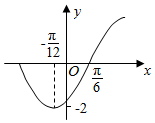
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
5.一个圆过点(-5,1)且圆心在直线2x+y+4=0上,求半径最小时的圆心坐标( )
| A. | (-1,-2) | B. | (-2,0) | C. | (-$\frac{5}{2}$,1) | D. | (-3,2) |
6.已知函数f(x)=ex-ax-1,g(x)=ln(ex-1)-lnx,若?x0∈(0,+∞),使得f(g(x0)>f(x0)成立,则a的取值范围是( )
| A. | (0,+∞) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
 如图,已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$,底面边长为3,求异面直线BC1与AC所成的角的大小.
如图,已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$,底面边长为3,求异面直线BC1与AC所成的角的大小.