题目内容
2．若直线l∥平面α，直线a?α，则l与a的位置关系是（ ）| A． | l∥a | B． | l与a异面 | C． | l与a相交 | D． | l与a没有公共点 |
分析 以正方体为载体，列举出所有可能结果，由此能求出结果．
解答 解：在正方体ABCD-A1B1C1D1中，
直线A1B1∥面ABCD，AB?面ABCD，A1B1∥AB；
直线A1B1∥面ABCD，AD?面ABCD，且A1B1与AD是异面直线．
∵直线l∥平面α，直线a?α，
∴l与a的位置关系是平面或异面，
∴l与a没有公共点．
故选：D．
点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
12．已知集合M={x|x≤1}，P={x|x＜t}，若M∪P=P，则实数t应该满足的条件是（ ）
| A． | t＞1 | B． | t≥1 | C． | t＜1 | D． | t≤1 |
13．已知全集U={1，2，3，4，5，6}，A={1，3，5}，B={2，3，4}，则（∁UA）∩B=（ ）
| A． | {2，4} | B． | { 3 } | C． | {2，4，6} | D． | {1，2，3，4，5} |
10．已知x与y之间的几组数据如表：
假设根据上表数据所得线性回归方程为$\widehat{y}$=$\widehat{b}$x+＜“m“：math xmlns：dsi='http://www．dessci．com/uri/2003/MathML'dsi：zoomscale='150'dsi：_mathzoomed='1'style='CURSOR：pointer； DISPLAY：inline-block'＞a^$\widehat{a}$，根据中间两组数据（4，3）和（5，4）求得的直线方程为y=bx+a，则$\widehat{b}$＜b，$\widehat{a}$＞a．（填“＞”或“＜”）
附：回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
附：回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
7．在150米高的山顶上，测得山下一塔的塔顶与塔底的俯角分别为30°，60°x=0，则塔高为（ ）
| A． | 50米 | B． | 75米 | C． | 100米 | D． | 125米 |
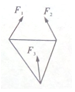如图，一块均匀的正三角形面的钢板的质量为10$\sqrt{6}$kg，在它的顶点处分别受力F1，F2，F3，每个力同它相邻的三角形的两边之间的角都是60°，且|F1|=|F2|=|F3|．要提起这块钢板，|F1|，|F2|，|F3|均要大于xkg，则x的最小值为$\frac{20\sqrt{2}}{3}$．
11．下列命题正确的是（ ）
| A． | 若x≠kπ，k∈Z，则 sin2x+$\frac{2}{si{n}^{2}x}$≥2$\sqrt{2}$ | B． | 若a＜0，则a+$\frac{4}{a}$≥-4 | ||
| C． | 若a＞0，b＞0，则lga+lgb$≥2\sqrt{lga•lgb}$ | D． | 若a＜0，b＜0，则$\frac{a}{b}+\frac{b}{a}≥2$ |