题目内容
17.连续抛掷两颗骰子,设第一颗向上点数为m,第二颗向上点数为n.(Ⅰ)求m-n=3的概率;
(Ⅱ)求m•n为偶数,且|m-n|<3的概率.
分析 抛两枚骰子共有36种结果,(Ⅰ)m-n=3的基本事件有3个,(Ⅱ)m•n为偶数,且|m-n|<3的基本事件有17个,由古典概型计算概率公式可得答案.
解答 解:(Ⅰ)抛掷两颗骰子所出现的不同结果数是6×6=36,事件“抛掷两颗骰子,所得两颗骰子的点数为m-n=3”所包含的基本事件有(4,1),(5,2),(6,3)共3个,故m-n=3的概率P=$\frac{3}{36}$=$\frac{1}{12}$,
(Ⅱ)m•n为偶数,且|m-n|<3的基本事件有(1,2),(2,1),(2,2),(2,3),(2,4),(3,2),(3,4),(4,2),(4,3),(4,4),(4,5),(4,6),(5,4),(5,6),(6,4),(6,5),(6,6)共17个,
故m•n为偶数,且|m-n|<3的概率P=$\frac{17}{36}$.
点评 本题考查古典概型及其概率计算公式,正确列举出所有基本事件是解决该题的关键.

练习册系列答案
相关题目
5.一个圆锥形漏斗的母线长为20,高为h,则体积V的表达式为( )
| A. | $\frac{1}{3}$π(400-h2)h | B. | π(400-h2)h | C. | $\frac{1}{3}$πh$\sqrt{400-{h}^{2}}$ | D. | πh$\sqrt{400-{h}^{2}}$ |
5.某班同学利用国庆节进行社会实践,对[20,50]岁的临汾市“低头族”(低头族电子产品而忽视人际交往的人群)人群随是因使用机抽取1000人进行了一次调查,得到如下频数分布表:
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计[20,50]年龄段的“低头族”的平均年龄(同一组中的数据用该组区间的中点值作代表);
(3)从年龄段在[25,35)的“低头族”中采用分层抽样法抽取6人接受采访,并从6人中随机选取2人作为嘉宾代表,求选取的2名嘉宾代表中恰有1人年龄在[25,30)岁的概率.
| 年龄段分组 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 频数 | 300 | 320 | 160 | 160 | 40 | 20 |
(2)估计[20,50]年龄段的“低头族”的平均年龄(同一组中的数据用该组区间的中点值作代表);
(3)从年龄段在[25,35)的“低头族”中采用分层抽样法抽取6人接受采访,并从6人中随机选取2人作为嘉宾代表,求选取的2名嘉宾代表中恰有1人年龄在[25,30)岁的概率.
2.准线为x=-2的抛物线的标准方程为( )
| A. | y2=-8x | B. | y2=8x | C. | x2=8y | D. | x2=-8y |
6.如图是一个几何体的三视图,则该几何体的体积等于( )
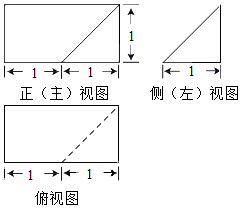

| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{5}{3}$ |
7.已知等差数列{an}的前n项和为Sn,a1+a5=0,且a9=20.则S11=( )
| A. | 260 | B. | 220 | C. | 130 | D. | 110 |