题目内容
6.如图是一个几何体的三视图,则该几何体的体积等于( )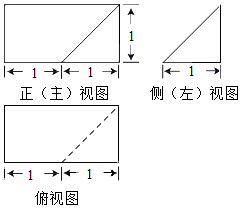
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{5}{3}$ |
分析 几何体为三棱柱切去一个三棱锥,使用作差法求出体积.
解答 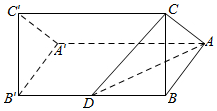 解:由三视图可知几何体为直三棱柱ABC-A′B′C′切去三棱锥D-ABC得到的,
解:由三视图可知几何体为直三棱柱ABC-A′B′C′切去三棱锥D-ABC得到的,
其中BC⊥平面ABB′A′,D为BB′中点,AB=BC=1,BB′=2.
∴三棱柱ABC-A′B′C′的体积为$\frac{1}{2}×$AB×BC×BB′=1,
三棱锥D-ABC的体积为$\frac{1}{3}×\frac{1}{2}×AB×BC×BD$=$\frac{1}{6}$,
∴几何体的体积V=1-$\frac{1}{6}$=$\frac{5}{6}$.
故选:B.
点评 本题考查了空间几何体的结构特征和三视图以及体积计算,属于基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
1.若位于x轴上方、且到点A(-2,0)和B(2,0)的距离的平方和为18的点的轨迹为曲线C,点P的坐标为(a,b),则“$b=\sqrt{5-{a^2}}$”是“点P在曲线C上”的( )
| A. | .充分不必要条件 | B. | .必要不充分条件 | ||
| C. | .充要条件 | D. | 既非充分又非必要条件 |
11.设函数f(x)=sinxcos2x,则下列结论中错误的为( )
| A. | 点(π,0)是函数y=f(x)图象的一个对称中心 | |
| B. | 直线x=$\frac{π}{2}$是函数y=f(x)图象的一条对称轴 | |
| C. | π是函数y=f(x)的周期 | |
| D. | 函数y=f(x)的最大值为1 |
18.某民营企业生产甲、乙两种产品,根据以往经验和市场调查,甲产品的利润与投入资金成正比,乙产品的利润与投入资金的算术平方根成正比,已知甲、乙产品分别投入资金4万元时,所获得利润(万元)情况如下:
该企业计划投入资金10万元生产甲、乙两种产品,那么可获得的最大利润(万元)是( )
| 投入资金 | 甲产品利润 | 乙产品利润 |
| 4 | 1 | 2.5 |
| A. | $\frac{9}{2}$ | B. | $\frac{65}{16}$ | C. | $\frac{35}{8}$ | D. | $\frac{17}{4}$ |
15.在△ABC中,内角A,B,C的对边分别为a,b,c,则“cosA=$\frac{b}{c}$”是“△ABC为Rt△”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
16.已知a,b∈R,则“|b|+a<0”是“b2<a2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点在抛物线y2=4$\sqrt{2}$x的准线上,离心率为$\frac{\sqrt{6}}{3}$,若不过椭圆E上顶点A的动直线l与椭圆E交于P、Q两点,且$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点在抛物线y2=4$\sqrt{2}$x的准线上,离心率为$\frac{\sqrt{6}}{3}$,若不过椭圆E上顶点A的动直线l与椭圆E交于P、Q两点,且$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0.