题目内容
若双曲线
-
=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、[-3,3] |
| B、(-∞,-3]∪[3,+∞) |
| C、[-5,5] |
| D、(-∞,5]∪[5,+∞) |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,由题意画出图形,利用点到直线的距离公式,即可求解m的取值范围.
解答:
解:双曲线
-
=1,渐近线为:y=±
x,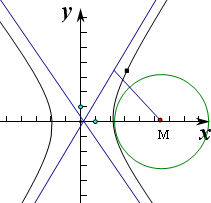
因为双曲线
-
=1-=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,
如图:只需圆心到直线的距离大于半径即可,
圆的圆心坐标(m,0)圆的半径为r=4,
所以圆心到直线的距离d=
=
≥4,
解得:m≥5或m≤-5.
实数m的取值范围是:{m|m≥5或m≤-5}.
故选:D
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |

因为双曲线
| x2 |
| 9 |
| y2 |
| 16 |
如图:只需圆心到直线的距离大于半径即可,
圆的圆心坐标(m,0)圆的半径为r=4,
所以圆心到直线的距离d=
| |4m| | ||
|
| |4m| |
| 5 |
解得:m≥5或m≤-5.
实数m的取值范围是:{m|m≥5或m≤-5}.
故选:D
点评:本题考查双曲线的简单性质的应用,圆的方程的应用以及线性规划的应用,考查分析问题解决问题的能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知一个球的直径为2,则该球的表面积是( )
| A、π | B、2π | C、3π | D、4π |
 如图,F1、F2是双曲线C:
如图,F1、F2是双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
二次函数f(x)=ax2+2a是区间[-a,a2]上的偶函数,又g(x)=f(x-1),则g(0),g(
),g(3)的大小关系是( )
| 3 |
| 2 |
A、g(
| ||
B、g(0)<g(
| ||
C、g(
| ||
D、g(3)<g(
|
对于函数f(x)=sin2x+sinxcosx下列说法正确的是( )
| A、该函数的最小正周期为2π | ||||
| B、该函数为偶函数 | ||||
C、该函数的一个单调增区间为(-
| ||||
D、该函数图象的一个对称中心是(
|
对于函数f(x)=sin(πx+
),下列命题正确的是( )
| π |
| 2 |
| A、f(x)是周期为2的偶函数 |
| B、f(x)是周期为π的偶函数 |
| C、f(x)是周期为2的奇函数 |
| D、f(x)是周期为π的奇函数 |
为了得到函数y=cos(2x+
)的图象,只需将函数y=sin2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
