题目内容
3.太阳光线与地面的夹角为30°,一个球在地面的影子是椭圆,那么椭圆的离心率为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
分析 首先要弄懂椭圆产生的原理,根据原理来解决三角形的边角关系,利用离心率公式求的结果.
解答 解:已知桌面上有一个球,半径为R,太阳光线与地面成30°角,
如图,l1和l2是两条与球相切的光线,分别切于点A和点C,分别与桌面交于点B和点D,则AC就是球的直径,BD的长就是椭圆的长轴长.过点A作AE∥BD,交l2于点E,则BD=AE.在Rt△AEC中,因为∠AEC=30°,所以AE=$\frac{2R}{sin30°}$,即a=$\frac{R}{sin30°}$,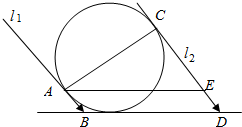
又因为b=R,所以c=$\sqrt{(\frac{R}{sin30°})^{2}-{R}^{2}}$=$\frac{Rcos30°}{sin30°}$,
所以e=cos30°=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查:椭圆产生的原理,a、b、c的关系式,求椭圆的离心率.

练习册系列答案
相关题目
15.若集合A={x|(x+1)(3-x)>0},集合B={x|1-x>0},则A∩B等于( )
| A. | (1,3) | B. | (-∞,-1) | C. | (-1,3) | D. | (-1,1) |
2.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,可求得该女子第3天所织布的尺数为( )
| A. | $\frac{20}{31}$ | B. | $\frac{3}{5}$ | C. | $\frac{8}{15}$ | D. | $\frac{2}{3}$ |
15.函数 f(x)=ex+a,g(x)=|ln(-x)|,若x1,x2都满足f(x)=g(x),则( )
| A. | x1•x2>e | B. | 1<x1•x2<e | C. | 0<x1x2<$\frac{1}{e}$ | D. | $\frac{1}{e}<{x_1}{x_2}$<1 |
13.已知:sin($\frac{π}{2}$+θ)+3cos(π-θ)=sin(-θ),则sinθcosθ+cos2θ=( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3}{5}$ |