题目内容
15.函数 f(x)=ex+a,g(x)=|ln(-x)|,若x1,x2都满足f(x)=g(x),则( )| A. | x1•x2>e | B. | 1<x1•x2<e | C. | 0<x1x2<$\frac{1}{e}$ | D. | $\frac{1}{e}<{x_1}{x_2}$<1 |
分析 根据题意,得出函数f(x)与g(x)在定义域(-∞,0)上有两个交点(x1,0)和(x2,0);
画出图形,结合图形得出0>x1>-1>x2,列出方程组$\left\{\begin{array}{l}{{e}^{{x}_{1}}+a=-ln({-x}_{1})}\\{{e}^{{x}_{2}}+a=ln({-x}_{2})}\end{array}\right.$,
从而得出ln(x1x2)=${e}^{{x}_{2}}$-${e}^{{x}_{1}}$;求出${e}^{{x}_{2}}$-${e}^{{x}_{1}}$的取值范围,即得x1x2的取值范围.
解答  解:∵f(x)=ex+a,g(x)=|ln(-x)|=$\left\{\begin{array}{l}{ln(-x),x≤-1}\\{-ln(-x),-1<x<0}\end{array}\right.$,
解:∵f(x)=ex+a,g(x)=|ln(-x)|=$\left\{\begin{array}{l}{ln(-x),x≤-1}\\{-ln(-x),-1<x<0}\end{array}\right.$,
且x1,x2都满足f(x)=g(x),
∴函数f(x)与g(x)在定义域(-∞,0)上有两个交点(x1,0)和(x2,0);如图所示,
不妨设0>x1>-1>x2,
则$\left\{\begin{array}{l}{{e}^{{x}_{1}}+a=-ln({-x}_{1})}\\{{e}^{{x}_{2}}+a=ln({-x}_{2})}\end{array}\right.$,
∴${e}^{{x}_{1}}$-${e}^{{x}_{2}}$=-ln(-x1)-ln(-x2)=-ln(x1x2),
即ln(x1x2)=${e}^{{x}_{2}}$-${e}^{{x}_{1}}$;
∵0>x1>-1>x2,
∴-1<${e}^{{x}_{2}}$-${e}^{{x}_{1}}$<0,
即-1<ln(x1x2)<0,
∴$\frac{1}{e}$<x1x2<1.
故选:D.
点评 本题考查了函数的图象与性质的应用问题,也考查了数形结合的解题思想,转化思想,是综合性题目.

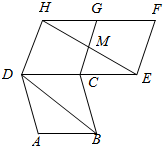 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B. | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C. | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D. | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 无数条 |
 如图,椭圆 M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形 A BCD的面积为$32\sqrt{3}$.
如图,椭圆 M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形 A BCD的面积为$32\sqrt{3}$.