7的展开式中x3y4与x4y3项的系数之比为$\frac{3}{4}$ 题目和参考答案——青夏教育精英家教网—

题目内容

15．（4x+3y）⁷的展开式中x³y⁴与x⁴y³项的系数之比为$\frac{3}{4}$ （用数字作答）

分析根据的形式展开式的通项公式，求出展开式中x³y⁴项与x⁴y³项的系数，计算比值即可．

解答解：（4x+3y）⁷展开式的通项公式为
T_r+1=${C}_{7}^{r}$•（4x）^7-r•（3y）^r=${C}_{7}^{r}$•4^7-r•3^r•x^7-r•y^r，
令r=4，得x³y⁴项的系数为${C}_{7}^{4}$•4³•3⁴，
令r=3，得x⁴y³项的系数为${C}_{7}^{3}$•4⁴•3³，
所以展开式中x³y⁴与x⁴y³项的系数之比为
$\frac{{C}_{7}^{4}{•4}^{3}{•3}^{4}}{{C}_{7}^{3}{•4}^{4}{•3}^{3}}$=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．

点评本题考查了利用二项式展开式的通项公式求特定项的应用问题，是基础题目．

练习册系列答案

16．设a，b∈R，则“a＞b”是“a（e^a+e^-a）＞b（e^b+e^-b）”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分又不必要条件

3．设$\overrightarrow{AB}$=（k，1）（k∈Z），$\overrightarrow{AC}$=（2，4），若k为满足|$\overrightarrow{AB}$|≤4的一个随机数，则△ABC是直角三角形的概率是（　　）

10．如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表．某人随机选择2月1日至2月13日中的某一天到该市出差，第二天返回（往返共两天）．

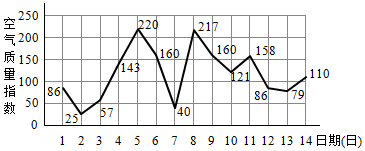
（Ⅰ）由图判断从哪天开始连续三天的空气质量指数方差最大？（只写出结论不要求证明）
（Ⅱ）求此人到达当日空气质量优良的概率；
（Ⅲ）设X是此人出差期间（两天）空气质量中度或重度重度污染的天数，求X的分布列与数学期望．

空气质量指数	污染程度
小于100	优良
大于100且小于150	轻度
大于150且小于200	中度
大于200且小于300	重度
大于300且小于500	严重
大于500	爆表

20．设f（x）是定义在R上的周期为3的函数，当x∈[0，2）时，f（x）=$\left\{\begin{array}{l}{3{x}^{2}-x，0≤x≤1}\\{2-x，1＜x＜2}\end{array}\right.$，则f（-$\frac{5}{2}$）=（　　）

7．命题“?n∈N^*，$\frac{1}{n}$＞$\frac{1}{n+1}$”的否定为（　　）

	A．	?n∈N^*，$\frac{1}{n}$≤$\frac{1}{n+1}$		B．	?n∈N^*，$\frac{1}{n}$＜$\frac{1}{n+1}$
	C．	?n∈N^*，$\frac{1}{{n}_{0}}$≤$\frac{1}{{n}_{0}+1}$		D．	?n₀∈N^*，$\frac{1}{{n}_{0}}$＜$\frac{1}{{n}_{0}+1}$

4．某城市100户居民的月平均用电量（单位：度）以[160，180），[180，200），[200，220），[220，240）[240，260），[260，280），[280，300]分组的频率分布直方图如图：

（1）求直方图中x的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量[240，260），[260，280），[280，300]的四组用户中，用分层抽样的方法抽取11户居民，则越平均用电量在[220，240）的用户中应抽取多少户？

5．

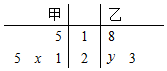甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图，甲乙两人的平均数与中位数分别相等，则x：y为（　　）

试题分类