题目内容
正四棱柱ABCD-A1B1C1D1的底面边长为2,若AC1与底面ABCD所成角为60°,则A1C1和底面ABCD的距离是 .
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:确定A1C1到底面ABCD的距离为正四棱柱ABCD-A1B1C1D1的高,即可求得结论.
解答:
 解:∵正四棱柱ABCD-A1B1C1D1,
解:∵正四棱柱ABCD-A1B1C1D1,
∴平面ABCD∥平面A1B1C1D1,
∵A1C1?平面A1B1C1D1,
∴A1C1∥平面ABCD
∴A1C1到底面ABCD的距离为正四棱柱ABCD-A1B1C1D1的高
∵正四棱柱ABCD-A1B1C1D1的底面边长为2,AC1与底面ABCD成60°角,
∴A1A=2
tan60°=2
故答案为:2
.
 解:∵正四棱柱ABCD-A1B1C1D1,
解:∵正四棱柱ABCD-A1B1C1D1,∴平面ABCD∥平面A1B1C1D1,
∵A1C1?平面A1B1C1D1,
∴A1C1∥平面ABCD
∴A1C1到底面ABCD的距离为正四棱柱ABCD-A1B1C1D1的高
∵正四棱柱ABCD-A1B1C1D1的底面边长为2,AC1与底面ABCD成60°角,
∴A1A=2
| 2 |
| 6 |
故答案为:2
| 6 |
点评:本题考查线面距离,确定A1C1到底面ABCD的距离为正四棱柱ABCD-A1B1C1D1的高是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=sin(2x+
)(x∈R)的最小正周期为( )
| π |
| 3 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
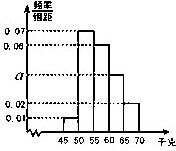 为了了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位为千克)全部介于45至70之间,将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70),得到如图所示的频率分布直方图,则a=
为了了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位为千克)全部介于45至70之间,将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70),得到如图所示的频率分布直方图,则a=