题目内容
3.设直线y=kx+1与圆x2+y2+2x-my=0相交于A,B两点,若点A,B关于直线l:x+y=0对称,则|AB|=$\sqrt{6}$.分析 直线y=kx+1与圆x2+y2+2x-my=0交于M、N两点,且M、N关于直线x+y=0对称,则直线x+y=0过圆心且与直线y=kx+1垂直,可求出k、m,利用点到直线的距离公式求出圆心到直线的距离,再由垂径定理求解|MN|.
解答 解:由题意可知,直线y=-x过圆心,且与直线y=kx+1垂直,
∴k=1,
圆x2+y2+2x-my=0的圆心坐标(-1,$\frac{m}{2}$)在直线x+y=0上,
∴-1$+\frac{m}{2}=0$,解得m=2,圆心坐标(-1,1),
x2+y2+2x-2y=0的半径r=$\frac{1}{2}\sqrt{{2}^{2}+(-2)^{2}-4×0}=\sqrt{2}$,
圆心到直线y=x+1的距离为$\frac{|-1-1+1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
因而弦长是$2\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查圆的一般方程,直线与圆位置关系的应用,训练了利用垂径定理求弦长,是中档题.

练习册系列答案
相关题目
13. 执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
 执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )| A. | 15 | B. | 12 | C. | 3 | D. | 180 |
14.(x2+$\frac{1}{2x}$)6的二项展开式中的常数项为( )
| A. | $\frac{15}{16}$ | B. | $\frac{3}{16}$ | C. | $\frac{15}{2}$ | D. | $\frac{15}{4}$ |
11.执行如图所示的程序框图,则输出S的值是( )


| A. | 145 | B. | 148 | C. | 278 | D. | 285 |
18.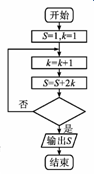 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )
 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )| A. | k>5? | B. | k>4? | C. | k>7? | D. | k>6? |
15.已知函数f(x)=$\frac{{lnx+{{(x-b)}^2}}}{x}$,若存在x∈[$\frac{1}{2}$,2],使得xf'(x)+f(x)>0,则实数b的取值范围是( )
| A. | $(-∞,\frac{3}{2})$ | B. | $(-∞,\frac{3}{2}]$ | C. | $(-∞,\frac{9}{4})$ | D. | $(-∞,\frac{9}{4}]$ |
12.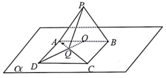 如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )
如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )
 如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )
如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )| A. | $\sqrt{-3+\frac{3\sqrt{7}}{2}}$ | B. | $\sqrt{3+\frac{3\sqrt{7}}{2}}$ | C. | $\sqrt{7}$ | D. | 3 |
13.设M={a|a=x2-y2,x,y∈Z},则对任意的整数n,形如4n,4n+1,4n+2,4n+3的数中,不是集合M中的元素是( )
| A. | 4n | B. | 4n+1 | C. | 4n+2 | D. | 4n+3 |