题目内容
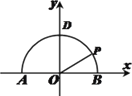
【题目】如图所示,定义域为![]() 上的函数
上的函数![]() 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.

(1)求![]() 的解析式;
的解析式;
(2)若![]() 关于的方程
关于的方程![]() 有三个不同解,求
有三个不同解,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的取值集合.
的取值集合.
【答案】(1)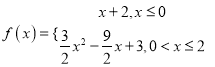 .;(2)
.;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由图象可知,当![]() 时,
时, ![]() 为一次函数;当
为一次函数;当![]() 时,
时, ![]() 是二次函数,分别用待定系数法求解析式;(2)当
是二次函数,分别用待定系数法求解析式;(2)当![]() 时,
时, ![]() ,结合图象可以得到当
,结合图象可以得到当![]() 时,函数
时,函数![]() 的图象和函数
的图象和函数![]() 的图象有三个公共点,即方程
的图象有三个公共点,即方程![]() 有三个不同解;(3)分
有三个不同解;(3)分![]() 和
和![]() 两种情况分别解方程即可。
两种情况分别解方程即可。
试题解析:
(1)①当![]() 时,函数
时,函数![]() 为一次函数,设其解析式为
为一次函数,设其解析式为![]() ,
,
∵点![]() 和
和![]() 在函数图象上,
在函数图象上,
∴![]()
解得![]()
![]()
②当![]() 时,函数
时,函数![]() 是二次函数,设其解析式为
是二次函数,设其解析式为![]() ,
,
∵点![]() 在函数图象上,
在函数图象上,
∴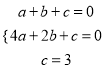
解得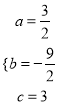
![]()
综上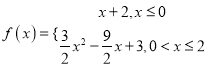 .
.
(2)由(1)得当![]() 时,
时, ![]() ,
,
∴![]() 。
。
结合图象可得若方程![]() 有三个不同解,则
有三个不同解,则![]() 。
。
∴实数![]() 的取值范围
的取值范围![]() .
.
(3)当![]() 时,由
时,由![]() 得
得![]()
解得 ![]() ;
;
当![]() 时,由
时,由![]() 得
得![]() ,
,
整理得![]()
解得![]() 或
或![]() (舍去)
(舍去)
综上得满足![]() 的
的![]() 的取值集合是
的取值集合是![]() .
.

练习册系列答案
相关题目