题目内容
13．已知f（2x+1）的定义域是[-1，3]，且f（x）的定义域由f（2x+1）确定，试求f（x）的定义域[-1，7]．分析 根据已知函数的定义域，求出2x+1的范围，就是所求函数的定义域．
解答 解：∵f（2x+1）的定义域是[-1，3]，
∴x∈[-1，3]，
∴2x+1∈[-1，7]，
∴f（x）的定义域是[-1，7]．
故答案为：[-1，7]．
点评 本题考查了求函数定义域的应用问题，解题时应弄清定义域是函数自变量的取值范围，是基础题目．
练习册系列答案
相关题目
3．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增．若实数a满足f（log2a）+f（${log_{\frac{1}{2}}}a$）≤2f（2），则a的取值范围是（ ）
| A． | （-∞，4] | B． | （0，4] | C． | $（0，\frac{1}{4}]$ | D． | $[\frac{1}{4}，4]$ |
4．已知函数$f（x）=\left\{\begin{array}{l}{2^{-x}}+1，x≤0\\{log_3}x+ax，x＞0\end{array}\right.$，若f（f（-1））＞4a，则实数a的取值范围是（ ）
| A． | （-∞，1） | B． | （-∞，0） | C． | $（-∞，-\frac{1}{5}）$ | D． | （1，+∞） |
8．下列函数是奇函数的是（ ）
| A． | f（x）=（x-1）$\sqrt{\frac{1+x}{1-x}}$ | B． | f（x）=$\frac{|x|}{x}$ | ||
| C． | f（x）=$\left\{\begin{array}{l}{1+x，（x≥0）}\\{1-x（x＜0）}\end{array}\right.$ | D． | f（x）=$\frac{1}{x-1}$ |
5．已知向量$\overrightarrow a$，$\overrightarrow b$满足$|{\overrightarrow a}|=2$，$|{\overrightarrow b}|=1$且$（{\overrightarrow a+\overrightarrow b}）⊥\overrightarrow b$，则$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{6}$ |
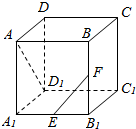长方体ABCD-A1B1C1D1中，AB=BC=2a，AA1=a，E和F分别是A1B1和BB1的中点，求：