题目内容
15．曲线f（x）=$\frac{1}{2}$x2在点（1，$\frac{1}{2}$）处的切线方程为（ ）| A． | 2x+2y+1=0 | B． | 2x+2y-1=0 | C． | 2x-2y-3=0 | D． | 2x-2y-1=0 |
分析 求出函数的导数，求得切线的斜率，由点斜式方程即可得到切线方程．
解答 解：f（x）=$\frac{1}{2}$x2的导数为f′（x）=x，
即有在点（1，$\frac{1}{2}$）处的切线斜率为1，
则在点（1，$\frac{1}{2}$）处的切线方程为y-$\frac{1}{2}$=x-1，
即为2x-2y-1=0．
故选：D．
点评 本题考查导数的运用：求切线方程，主要考查导数的几何意义，运用点斜式方程和正确求导是解题的关键．
练习册系列答案
相关题目
5．已知某几何体的三视图如图所示，则这个几何体的外接球的表面积等于（ ）
| A． | $\frac{7}{3}π$ | B． | 16π | C． | 8π | D． | $\frac{28}{3}π$ |
6．
如图Rt△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点P∈l，当点P逐渐远离点A时，∠PBC的大小（ ）
如图Rt△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点P∈l，当点P逐渐远离点A时，∠PBC的大小（ ）| A． | 不变 | B． | 变小 | ||
| C． | 变大 | D． | 有时变大有时变小 |
如图，四棱锥P-ABCD的底面ABCD为矩形，PA⊥底面ABCD，BC=4，AB=PA=2，M为线段PC的中点，N在线段BC上，且BN=1．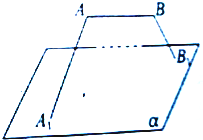
线段AB与平面α平行，α的斜线A1A、B1B与α所成的角分别为30°和60°，且∠A1AB=∠B1BA=90°，AB=2，A1B1=4，求AB与平面α的距离．