题目内容
已知数列{an}的前n项和Sn=2an-1(n∈N*),
(1)求an;
(2)设bn=
,Tn=b1+b2+b3+…+bn,若Tm+bm-1>
成立,求正整数m的最大值.
(1)求an;
(2)设bn=
| 3 |
| an•an+2 |
| 1 |
| 2014 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由Sn=2an-1,得Sn-1=2an-1-1(n≥2),S1=a1=2a1-1,从而{an}是首项为1,公比为2的等比数列,由此能求出an=2n-1.
(2)由bn=
=
=
,得Tn=1-
,从而
>
,由此能求出正整数m的最大值.
(2)由bn=
| 3 |
| an•an+2 |
| 3 |
| 2n-1•2n+1 |
| 3 |
| 4n |
| 1 |
| 4n |
| 2 |
| 4m |
| 1 |
| 2014 |
解答:
解:(1)∵数列{an}的前n项和Sn=2an-1(n∈N*),①
∴Sn-1=2an-1-1(n≥2),②
①-②,得:an=2an-2an-1,
整理,得an=2an-1,
又S1=a1=2a1-1,解得a1=1,
∴{an}是首项为1,公比为2的等比数列,
∴an=2n-1.
(2)∵bn=
=
=
,
∴Tn=b1+b2+b3+…+bn=
+
+
+…+
=
=1-
,
∵Tm+bm-1>
成立,
∴1-
+
-1>
,即
>
,
解得m<6,∵m∈N*,∴正整数m的最大值是5.
∴Sn-1=2an-1-1(n≥2),②
①-②,得:an=2an-2an-1,
整理,得an=2an-1,
又S1=a1=2a1-1,解得a1=1,
∴{an}是首项为1,公比为2的等比数列,
∴an=2n-1.
(2)∵bn=
| 3 |
| an•an+2 |
| 3 |
| 2n-1•2n+1 |
| 3 |
| 4n |
∴Tn=b1+b2+b3+…+bn=
| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 43 |
| 3 |
| 4n |
=
| ||||
1-
|
| 1 |
| 4n |
∵Tm+bm-1>
| 1 |
| 2014 |
∴1-
| 1 |
| 4m |
| 3 |
| 4m |
| 1 |
| 2014 |
| 2 |
| 4m |
| 1 |
| 2014 |
解得m<6,∵m∈N*,∴正整数m的最大值是5.
点评:本题主要考查数列的通项公式的求法、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想.

练习册系列答案
相关题目
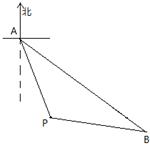 如图,某船在A处看见灯塔P在南偏东15°方向,后来船沿南偏东45°的方向航行30km后,到达B处,看见灯塔P在船的西偏北15°方向,则这时船与灯塔的距离是( )
如图,某船在A处看见灯塔P在南偏东15°方向,后来船沿南偏东45°的方向航行30km后,到达B处,看见灯塔P在船的西偏北15°方向,则这时船与灯塔的距离是( )| A、10km | ||
| B、20km | ||
C、10
| ||
D、5
|
(函数的定义域)函数y=log2(1+x)+
的定义域为( )
| 4-2x |
| A、(-1,2) |
| B、(0,2] |
| C、(0,2) |
| D、(-1,2] |
已知双曲线的一个焦点与抛物线x2=8y的焦点重合,且其渐近线的方程为
x±y=0,则该双曲线的标准方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|