题目内容
计算:|x2-
|<2x.
| 1 |
| 2 |
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:原不等式即为
或
,运用二次不等式的解法,即可得到解集.
|
|
解答:
解:|x2-
|<2x即为
或
,
即有
或
,
即
≤x<1+
或
-1<x<
.
则解集为[
,1+
)∪(
-1,
),
即为(
-1,1+
).
| 1 |
| 2 |
|
|
即有
|
|
即
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
则解集为[
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
即为(
| ||
| 2 |
| ||
| 2 |
点评:本题考查绝对值不等式的解法,考查绝对值的定义,考查运算能力,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知复数z满足(3+i)z=i,则z=( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
在区域
内任取一点P,则点P落在单位圆x2+y2=1内的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
下列双曲线中,渐近线方程是y=±
x的是( )
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=cosx的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移
个单位,所得函数图象的一条对称轴方程是( )
| π |
| 4 |
| A、x=π | ||
B、x=
| ||
C、x=
| ||
D、x=
|
阅读程序框图,若m、n分别是双曲线
-
=1的虚轴长和实半轴长,则输出a,i别是( ) 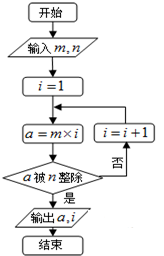
| x2 |
| 36 |
| y2 |
| 4 |

| A、a=12,i=3 |
| B、a=12,i=4 |
| C、a=8,i=3 |
| D、a=8,i=4 |