题目内容
2.设方程x2-$\sqrt{10}$x+2=0的两根为α、β,求$lo{g}_{2}\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$的值.分析 首先根据一元二次方程求出α+β=$\sqrt{10}$,α•β=2,进一步对关系式$\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$进行恒等变换,最后求出结果.
解答 解:α、β是方程x2-$\sqrt{10}$x+2=0的两实根,
则:α+β=$\sqrt{10}$,α•β=2.
故:$\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$=$\frac{(α+β)^{2}-3αβ}{(α+β)^{2}-4αβ}$=2,
则:$lo{g}_{2}\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$=1.
点评 本题考查的知识要点:一元二次方程的根和系数的关系,对数的运算和式子的恒等变形问题.

练习册系列答案
相关题目
13.已知a>0且a≠1,f(x)+g(x)=ax-a-x+2,其中f(x)为R上的奇函数,g(x)为R上的偶函数,若g(2)=a,则f(2)的值为( )
| A. | 2 | B. | 1 | C. | $\frac{17}{4}$ | D. | $\frac{15}{4}$ |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),P为双曲线上任一点,若双曲线的离心率的取值范围为[$\sqrt{2}$,2],则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$最小值的取值范围是( )
| A. | [$\frac{1}{2}$,$\frac{3}{4}$] | B. | [-$\frac{3}{4}$,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,-$\frac{1}{4}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$] |
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0,且关于x的函数f(x)=2x3-3|$\overrightarrow{a}$|x2+6$\overrightarrow{a}$•$\overrightarrow{b}$x+5在实数集R上有极值,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的取值范围是( )
| A. | ($\frac{π}{3}$,π) | B. | ($\frac{π}{3}$,π] | C. | [$\frac{π}{3}$,π] | D. | (0,$\frac{π}{3}$) |
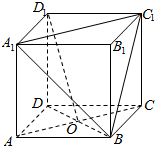 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.