题目内容
已知平面平域D由下列约束条件确定：2x-3y+5≥0，x+2y-8≤0，x-5y+6≥0，当点（x，y）在D上时，
（1）若z=3x-4y，则z的最大值是 ，最小值是 ；
（2）当z=x2+y2时，则z的最大值是 ，最小值是 ．
（1）若z=3x-4y，则z的最大值是
（2）当z=x2+y2时，则z的最大值是
考点：简单线性规划
专题：计算题,作图题,不等式的解法及应用
分析：作出平面区域，
（1）化z=3x-4y为y=
x-
，利用几何意义解答；
（2）z=x2+y2可理解为点（x，y）到原点A的距离的平方，先求距离．
（1）化z=3x-4y为y=
| 3 |
| 4 |
| z |
| 4 |
（2）z=x2+y2可理解为点（x，y）到原点A的距离的平方，先求距离．
解答：
解：作出平面区域如下图：
由图可知，三个交点分别是D（2，3），E（4，2），C（-1，1），
（1）在点E（4，2）处时，z有最大值为3×4-4×2=4，
在点C（-1.1）处时，z有最小值为3×（-1）-4×1=-7，
（2）z=x2+y2可理解为点（x，y）到原点A的距离的平方，
距离的最大为
=2
，最小为
．
故z=x2+y2的最大值为20，最小值为
．
故答案为：（1）4，-7；（2）20，
．
由图可知，三个交点分别是D（2，3），E（4，2），C（-1，1），
（1）在点E（4，2）处时，z有最大值为3×4-4×2=4，
在点C（-1.1）处时，z有最小值为3×（-1）-4×1=-7，
（2）z=x2+y2可理解为点（x，y）到原点A的距离的平方，
距离的最大为
| 42+22 |
| 5 |
|
故z=x2+y2的最大值为20，最小值为
| 18 |
| 13 |
故答案为：（1）4，-7；（2）20，
| 18 |
| 13 |
点评：本题考查了线性规划问题，注意目标函数的几何意义是解决问题的关键．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
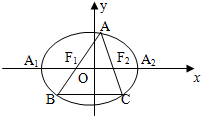如图：A1、A2是椭圆