题目内容
双曲线
-
=1(a>0,b>0)的左、右顶点分别为A、B,渐近线分别为l1、l2,点P在第一象限内且在l1上,若PA⊥l2,PB∥l2,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:求出双曲线的顶点和渐近线方程,设P(m,
m),再由两直线垂直和平行的条件,得到m,a,b的关系式,消去m,可得a,b的关系,再由离心率公式计算即可得到.
| b |
| a |
解答:
解:双曲线
-
=1(a>0,b>0)的左、右顶点分别为A(-a,0)、B(a,0),
渐近线分别为l1:y=
x,l2:y=-
x.
设P(m,
m),若PA⊥l2,PB∥l2,
则
•(-
)=-1①,且
=-
,②
由②可得m=
,
代入①可得b2=3a2,
即有c2-a2=3a2,即c=2a,
则有e=
=2.
故选B.
| x2 |
| a2 |
| y2 |
| b2 |
渐近线分别为l1:y=
| b |
| a |
| b |
| a |
设P(m,
| b |
| a |
则
| ||
| m+a |
| b |
| a |
| ||
| m-a |
| b |
| a |
由②可得m=
| a |
| 2 |
代入①可得b2=3a2,
即有c2-a2=3a2,即c=2a,
则有e=
| c |
| a |
故选B.
点评:本题考查双曲线的方程和性质,主要考查双曲线的渐近线方程和离心率的求法,运用两直线垂直的条件和平行的条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知下列各组命题,其中p是q的充分必要条件的是( )
| A、p:m≤-2或m≥6;q:y=x2+mx+m+3 有两个不同的零点 | ||
B、p:
| ||
| C、p:cosα=cosβ;q:tanα=tanβ | ||
| D、p:A∩B=A; q:A⊆U,B⊆U,∁UB⊆∁UA |
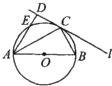 如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为
如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为