题目内容
4.命题“?x∈R,x2+2x+2<0”的否定是?x∈R,x2+2x+2≥0.分析 直接利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,所以,命题“?x∈R,x2+2x+2<0”的否定是:?x∈R,x2+2x+2≥0.
故答案为:?x∈R,x2+2x+2≥0.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
相关题目
15.下列各图中,表示以x为自变量的奇函数的图象是( )
| A. | 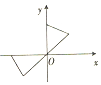 | B. | 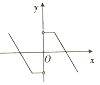 | C. |  | D. |  |
13.函数y=x2(x-3)的单调递减区间是( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,2) | D. | (-2,2) |
14.各项都是正数的等比数列{an}的公比q≠1,${a_1},\frac{1}{2}{a_3},{a_2}_{\;}$成等差数列,则$\frac{{{a_3}+{a_4}}}{{{a_4}+{a_5}}}$=( )
| A. | $\frac{{-1+\sqrt{3}}}{2}$ | B. | $\frac{{-1+\sqrt{5}}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $2+\sqrt{5}$ |
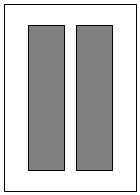 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm