Question

已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
（1）求证：平面CDE⊥平面ABC
（2）若AB=DC=3，BC=5，BD=4，求几何体ABCD的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定

专题：计算题

分析：（1）先证出直线AB与平面上的两条相交直线垂直，得到线面垂直，而线又在一个平面上，得到面面垂直．
（2）要求的几何体是一个三棱锥，线段CD的长是三棱锥C-ABD的高，做出对应的底面的面积，根据三棱锥的体积公式做出结果

解答： 解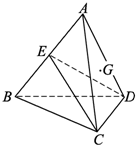：（1）证明：∵BC=AC，E为AB的中点，
∴AB⊥CE．
又∵AD=BD，E为AB的中点
∴AB⊥DE．
∵DE∩CE=E
∴AB⊥平面DCE
∵AB?平面ABC，
∴平面CDE⊥平面ABC．
（2）∵在△BDC中，DC=3，BC=5，BD=4，
∴CD⊥BD，
在△ADC中，DC=3，AD=BD=4，AC=BC=5，
∴CD⊥AD，
∵AD∩BD=D∴CD⊥平面ABD．所以线段CD的长
是三棱锥C-ABD的高
又在△ADB中，DE=

16- 9 4

=

55

2

∴V_C-ABD=

1

3

×

1

2

×3×

55

2

×3=

3 55

4

．

点评：本题考查空间几何体的点线面之间的关系的证明，锥体体积的计算，关键是熟练所学的判定定理和性质定理．