题目内容
定义max[a，b]=
，f（x）=max[（x-2）2，|x|]，则f（x）的最小值为 ．
|
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：由已知中max[a，b]=
，画出函数f（x）=max[（x-2）2，|x|]的图象，借助图象可得答案．
|
解答：
解：∵max[a，b]=
，
∴f（x）=max[（x-2）2，|x|]的图象如下图所示：
由图可得：f（x）的最小值为：1，
故答案为：1
|
∴f（x）=max[（x-2）2，|x|]的图象如下图所示：
由图可得：f（x）的最小值为：1，
故答案为：1
点评：本题考查的知识点是函数的最值及其几何意义，其中画出函数f（x）=max[（x-2）2，|x|]的图象，是解答的关键．
练习册系列答案
相关题目
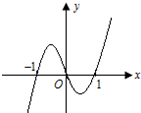已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），则以下说法错误的是（ ）| A、f′（1）+f′（-1）=0 |
| B、当x=-1时，函数f（x）取得极大值 |
| C、方程xf'（x）=0与f（x）=0均有三个实数根 |
| D、当x=1时，函数f（x）取得极小值 |