题目内容
1.已知函数f(x)=sinωx(其中ω>0)图象过(π,-1)点,且在区间(0,$\frac{π}{3}$)上单调递增,则ω的值为$\frac{3}{2}$.分析 根据函数过点,得到ω=2k-$\frac{1}{2}$,然后结合函数单调性的关系建立不等式条件,进行求解即可.
解答 解:∵函数f(x)=sinωx(其中ω>0)图象过(π,-1)点,
∴f(π)=sinπω=-1,
即πω=2kπ-$\frac{π}{2}$,即ω=2k-$\frac{1}{2}$,
∵在区间(0,$\frac{π}{3}$)上单调递增,
∴$\frac{1}{4}$T=$\frac{1}{4}•\frac{2π}{ω}$≥$\frac{π}{3}$,
即2ω≤3,则0<ω≤$\frac{3}{2}$,
则当k=1时,ω=$\frac{3}{2}$,满足条件.
故答案为:$\frac{3}{2}$.
点评 本题主要考查三角函数单调性的应用,根据函数单调性和周期之间的关系是解决本题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
12. 某市乘坐出租车的收费办法如下:
某市乘坐出租车的收费办法如下:
不超过4千米的里程收费12元;超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);当车程超过4千米时,另收燃油附加费1元.
相应系统收费的程序框图如图所示,其中x(单位:千米)为行驶里程,y(单位:元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
 某市乘坐出租车的收费办法如下:
某市乘坐出租车的收费办法如下:不超过4千米的里程收费12元;超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);当车程超过4千米时,另收燃油附加费1元.
相应系统收费的程序框图如图所示,其中x(单位:千米)为行驶里程,y(单位:元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
| A. | $y=2[x-\frac{1}{2}]+4$ | B. | $y=2[x-\frac{1}{2}]+5$ | C. | $y=2[x+\frac{1}{2}]+4$ | D. | $y=2[x+\frac{1}{2}]+5$ |
16.关于函数f(x)=|sinx|+|cosx|,给出下列三个结论:
①函数f(x)的最小值是1;
②函数f(x)的最大值是$\sqrt{2}$;
③函数f(x)在区间(0,$\frac{π}{4}$)上单调递增.
其中全部正确结论的序号是( )
①函数f(x)的最小值是1;
②函数f(x)的最大值是$\sqrt{2}$;
③函数f(x)在区间(0,$\frac{π}{4}$)上单调递增.
其中全部正确结论的序号是( )
| A. | ② | B. | ②③ | C. | ①③ | D. | ①②③ |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(α>0,b>0)的左右焦点为F1,F2,|F1F2|=2$\sqrt{5}$,点P是双曲线右支上一点,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=10,在△PF1F2中,∠PF1F2的角平分线与另外两个角的外角平分线交于一点Q,Q点横坐标为4,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{15}}{3}$ |
10.设F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点A是以F1F2为直径的圆与双曲线在第一象限的交点,延长AF2与双曲线交于点B,若|BF2|=3|AF2|,则此双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\sqrt{10}$ | D. | 3 |
11.某高科技公司对某种新研制的产品进行售后调查,对其50天内的日销售量(单位:吨)进行统计,结果如下:
已知每天的销售量相互独立.
(1)求5天中该种商品恰好有三天的销售量不为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元,X表示该种商品某两天销售利润的和(单位:千元),若某两天的利润和超过这50天的利润的数学期望,则称这两天为“黄金双天”.若某两天的利润和为6.4千元,试判断该两天是不是“黄金双天”.
已知每天的销售量相互独立.
| 日销售量 | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
(2)已知每吨该商品的销售利润为2千元,X表示该种商品某两天销售利润的和(单位:千元),若某两天的利润和超过这50天的利润的数学期望,则称这两天为“黄金双天”.若某两天的利润和为6.4千元,试判断该两天是不是“黄金双天”.
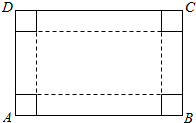 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).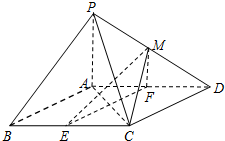 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=6,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=6,E,F分别为BC,AD的中点,点M在线段PD上.